The TPSPLNEV subroutine evaluates the thin-plate smoothing spline (TPSS) at new data points. It is used after the TPSPLINE subroutine fits a thin-plate spline model to data.

The TPSPLNEV subroutine returns the following value:

pred

is an 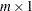vector of the predicated values of the TPSS fit evaluated at new data points.

The input arguments to the TPSPLNEV subroutine are as follows:

xpred

is an 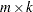matrix of data points at which the is evaluated, where is the number of new data points and 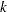is the number of variables in the spline model.

x

is an 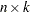matrix of design points that is used as an input of TPSPLINE call.

coeff

is the coefficient vector returned from the TPSPLINE call.

See the previous section on the TPSPLINE call for details about the TSPLNEV subroutine.

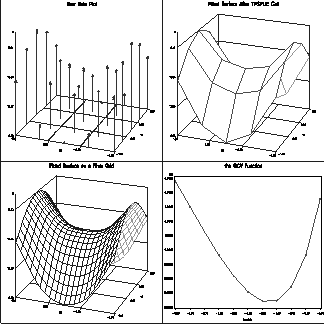
As an example, consider the following data set, which consists of two independent variables. The plot of the raw data can be found in the first panel of Figure 23.224.

   x={ -1.0 -1.0,    -1.0 -1.0,    -0.5 -1.0,    -0.5 -1.0,
        0.0 -1.0,     0.0 -1.0,     0.5 -1.0,     0.5 -1.0,
        1.0 -1.0,     1.0 -1.0,    -1.0 -0.5,    -1.0 -0.5,
       -0.5 -0.5,    -0.5 -0.5,     0.0 -0.5,     0.0 -0.5,
        0.5 -0.5,     0.5 -0.5,     1.0 -0.5,     1.0 -0.5,
       -1.0  0.0,    -1.0  0.0,    -0.5  0.0,    -0.5  0.0,
        0.0  0.0,     0.0  0.0,     0.5  0.0,     0.5  0.0,
        1.0  0.0,     1.0  0.0,    -1.0  0.5,    -1.0  0.5,
       -0.5  0.5,    -0.5  0.5,     0.0  0.5,     0.0  0.5,
        0.5  0.5,     0.5  0.5,     1.0  0.5,     1.0  0.5,
       -1.0  1.0,    -1.0  1.0,    -0.5  1.0,    -0.5  1.0,
        0.0  1.0,     0.0  1.0,     0.5  1.0,     0.5  1.0,
        1.0  1.0,     1.0  1.0 };

   y = {15.54, 15.76, 18.67, 18.50, 19.66, 19.80, 18.60, 18.52,
        15.87, 16.04, 10.92, 11.14, 14.81, 14.83, 16.56, 16.44,
        14.91, 15.06, 10.92, 10.94,  9.61,  9.65, 14.03, 14.03,
        15.77, 16.00, 14.00, 14.03,  9.56,  9.58, 11.21, 11.09,
        14.84, 14.99, 16.55, 16.51, 14.98, 14.72, 11.15, 11.17,
        15.83, 15.96, 18.64, 18.56, 19.54, 19.81, 18.57, 18.61,
        15.87, 15.90 };

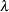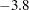Now generate a sequence of from to 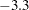so that you can study the GCV function within this range. Use the following statement:

   lambda = T( do(-3.8, -3.3, 0.1) );

Use the following statement to do the thin-plate smoothing spline fit and returning the fitted values on those design points.

   call tpspline(fit, coef, adiag, gcv, x, y, lambda);

The output from this call follows.

                   SUMMARY OF TPSPLINE CALL

        Number of observations                    50
        Number of unique design points            25
        Dimension of polynomial Space              3
        Number of Parameters                      28

        GCV Estimate of Lambda              0.00000668
        Smoothing Penalty                   2558.14323
        Residual Sum of Squares                0.24611
        Trace of (I-A)                        25.40680
        Sigma^2 estimate                       0.00969
        Sum of Squares for Replication         0.24223

After this TPSPLINE call, you obtained the fitted value. The fitted surface is plotted in the second panel of Figure 23.224. Also in Figure 23.224, panel 4, you plot the GCV function values against lambda. From panel 2, you see that because of the spare design points, the fitted surface is a little bit rough. In order to study the TPSS fit 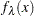more closely, you can use the following statements to generate a more dense grid on .

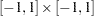   xGrid = T( do(-1, 1, 0.1) );
   yGrid = T( do(-1, 1, 0.1) );
   do i = 1 to nrow(xGrid);
      x1 = x1 // repeat(xGrid[i], nrow(yGrid));
      x2 = x2 // yGrid;
   end;
   xpred = x1 || x2;

Now you can use the function TPSPLNEV to evaluate 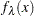on this dense grid. Here is the statement:

   call tpsplnev(pred, xpred, x, coef);

The final fitted surface is plotted in Figure 23.224, panel 3.

Figure 23.224 Plots of Fitted Surface