The ORVEC subroutine provides columnwise orthogonalization and stepwise QR decomposition by using the Gram-Schmidt process.

The ORTVEC subroutine returns the following values:

w

If the Gram-Schmidt process converges (lindep=0), 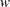is the 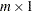vector 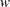orthonormal to the columns of 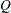, which is assumed to have 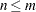(nearly) orthonormal columns. If the Gram-Schmidt process does not converge (lindep=1), 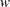is a vector of missing values. For stepwise QR decomposition, 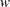is the th orthogonal column of the matrix 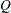. If there is no matrix 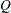, that is, if the 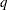argument is not specified, 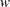is the normalized value of the vector ,

r

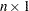If the Gram-Schmidt process converges (lindep=0), specifies the vector of Fourier coefficients. If the Gram-Schmidt process does not converge (lindep=1), is a vector of missing values. If the 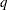argument is not specified, is a vector with zero dimension. For stepwise QR decomposition, contains the upper triangular elements of the th column of .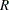

rho

If the Gram-Schmidt process converges (lindep=0), rho (often indicated by the Greek symbol, 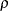) specifies the distance from 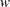to the range of 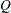. Even if the Gram-Schmidt process converges, if 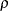is sufficiently small, the vector can be linearly dependent on the columns of 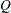. If the Gram-Schmidt process does not converge (lindep=1), 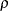is set to 0. For stepwise QR decomposition, 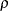contains the diagonal element of the th column of .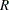

lindep

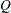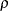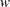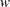returns a value of 1 if the Gram-Schmidt process does not converge in 10 iterations. In most cases, if lindep=1, the input vector is linearly dependent on the columns of the input matrix . In that case, is set to 0, and the results and contain missing values. If lindep=0, the Gram-Schmidt process did converge, and the results , , and 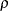are computed.

The input arguments to the ORTVEC subroutine are as follows:

v

specifies an 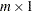vector that is to be orthogonalized to the columns of 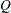. For stepwise QR decomposition of a matrix, is the th matrix column before its orthogonalization.

q

specifies an optional 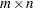matrix 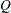that is assumed to have 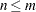(nearly) orthonormal columns. Thus, the matrix 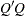should approximate the identity matrix. The column orthonormality assumption is not tested in the ORTVEC call. If it is violated, the results are not predictable. The argument 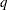can be omitted or can have zero rows and columns. For stepwise QR decomposition of a matrix, 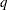contains the first matrix columns that are already orthogonal.

The relevant formula for the ORTVEC subroutine is

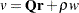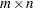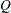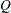Assuming that the matrix has (nearly) orthonormal columns, the ORTVEC subroutine orthogonalizes the vector to the columns of . The vector is the array of Fourier coefficients, and 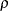is the distance from 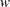to the range of .

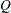There are two special cases:

• If , ORTVEC normalizes the result 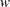, so that .

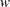• If , the output vector is the null vector.

The case 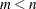is not possible since 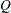is assumed to have (nearly) orthonormal columns.

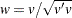To initialize a stepwise QR decomposition, ORTVEC can be called to normalize only, that is, to compute and 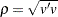only. There are two ways of using the ORTVEC call for this reason:

• Omit the last argument 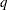, as in call ortvec(w,r,rho,lindep,v);.

• Provide a matrix 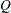with zero rows and columns, for example, by using the free q; command.

In both cases, is a column vector with zero rows.

The ORTVEC subroutine is useful for the following applications:

• performing stepwise QR decomposition. Compute 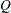and 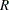, so that 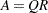, where 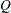is column orthonormal, , and 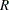is upper triangular. The 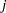th step is applied to the 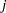th column, , of 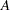, and it computes the 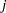th column 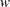of 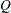and the 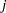th column, 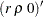, of .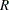

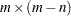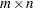• computing the null space matrix, , corresponding to an range space matrix,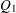 , by the following stepwise process: set 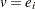(where is the 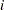th unit vector) and try to make it orthogonal to all column vectors of 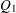and the already generated , if the subroutine is successful, append 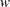to ; otherwise, try .

The 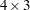matrix 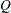contains the unit vectors 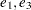, and 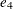. The column vector is pairwise linearly independent with the three columns of 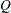. As expected, the ORTVEC call computes the vector 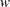as the unit vector with and .

   q = { 1  0  0,
         0  0  0,
         0  1  0,
         0  0  1 };
   v = { 1, 1, 1, 1 };
   call ortvec(w,u,rho,lindep,v,q);
   print rho u w;

You can perform the QR decomposition of the linearly independent columns of an 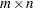matrix 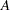with the following statements:

   a = { . . . enter matrix A here . . . };
   nind = 0;  ndep = 0;  dmax = 0.;
   n = ncol(a);  m = nrow(a);
   free q;
   do j = 1 to n;
      v = a[ ,j];
      call ortvec(w,u,rho,lindep,v,q);
      aro = abs(rho);
      if aro > dmax then dmax = aro;
      if aro <= 1.e-10 * dmax then lindep = 1;
      if lindep = 0 then do;
         nind = nind + 1;
         q = q || w;
         if nind = n then r = r || (u // rho);
         else r = r || (u // rho // j(n-nind,1,0.));
      end;
      else do;
         print "Column " j " is linearly dependent.";
         ndep = ndep + 1; ind[ndep] = j;
      end;
   end;

Next, process the remaining columns of :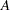

   do j = 1 to ndep;
      k = ind[ndep-j+1];
      v = a[ ,k];
      call ortvec(w,u,rho,lindep,v,q);
      if lindep = 0 then do;
         nind = nind + 1;
         q = q || w;
         if nind = n then r = r || (u // rho);
         else r = r || (u // rho // j(n-nind,1,0.));
      end;
   end;

Now compute the null space in the last columns of :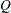

   do i = 1 to m;
      if nind < m then do;
        v = j(m,1,0.); v[i] = 1.;
        call ortvec(w,u,rho,lindep,v,q);
        aro = abs(rho);
        if aro > dmax then dmax = aro;
        if aro <= 1.e-10 * dmax then lindep = 1;
        if lindep = 0 then do;
          nind = nind + 1;
          q = q || w;
        end;
        else print "Unit vector" i "linearly dependent.";
      end;
   end;
   if nind < m then do;
      print "This is theoretically not possible.";
   end;