| Language Reference |
| BRANKS Function |
The BRANKS function computes the tied ranks and the bivariate ranks for an  matrix and returns an
matrix and returns an  matrix of these ranks. The tied ranks of the first column of matrix are contained in the first column of the result matrix; the tied ranks of the second column of matrix are contained in the second column of the result matrix; and the bivariate ranks of matrix are contained in the third column of the result matrix.
matrix of these ranks. The tied ranks of the first column of matrix are contained in the first column of the result matrix; the tied ranks of the second column of matrix are contained in the second column of the result matrix; and the bivariate ranks of matrix are contained in the third column of the result matrix.
The tied rank of an element 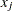 of a vector is defined as
of a vector is defined as
 |
where
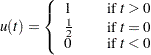 |
The bivariate rank of a pair 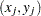 is defined as
is defined as
 |
The results of the BRANKS function can be used to compute rank-based correlation coefficients such as the Spearman rank-order correlation and Hoeffding’s 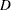 statistic.
statistic.
The following statements compute the bivariate ranks of two columns of data:
z = { 1 2,
2 1,
3 3,
3 5,
4 4,
5 4,
5 4,
4 5 };
b = branks(z);
print b;
Copyright © SAS Institute, Inc. All Rights Reserved.