| Language Reference |
| Power Operator, Matrix: ** |
- matrix ** scalar ;
The matrix power operator (**) creates a new matrix that is matrix multiplied by itself scalar times. The matrix argument must be square; scalar must be an integer greater than or equal to 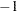 . If the scalar is not an integer, it is truncated to an integer.
. If the scalar is not an integer, it is truncated to an integer.
For example, the following statements compute a matrix that is the result of multiplying a matrix by itself. The result is shown in Figure 23.21.
a = {1 2,
1 1};
c = a**2;
print c;
Note that the expression a**(-1) is shorthand for matrix inversion, as shown by the following statements:
inv = a**(-1); /* shorthand for matrix inversion */ ident = inv * a; print inv, ident;
The matrix power operator does not support missing values.
Raising a matrix to a large power can cause numerical precision problems. If the matrix is symmetric, it is preferable to operate on its eigenvalues (see the EIGEN call) rather than to use the matrix power operator directly on the matrix, as shown in the following example:
b = {2 1,
1 1};
call eigen(lambda, E, b); /* recall that b = E*diag(lambda)*E` */
power = 20;
d = lambda##power;
a20 = E*diag(d)*E`; /* a**20 since E`*E = Identity */
print a20;
Copyright © SAS Institute, Inc. All Rights Reserved.