Example 9.7 Response Surface Methodology

A regression model with a complete quadratic set of regressions across several factors can be processed to yield the estimated critical values that can optimize a response. First, the regression is performed for two variables according to the model

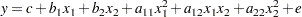The estimates are then divided into a vector of linear coefficients (estimates) 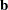and a matrix of quadratic coefficients 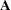. The solution for critical values is

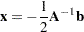The following program creates a module to perform quadratic response surface regression.

   /*          Quadratic Response Surface Regression            */
   /* This matrix routine reads in the factor variables and     */
   /* the response, forms the quadratic regression model and    */
   /* estimates the parameters, and then solves for the optimal */
   /* response, prints the optimal factors and response, and    */
   /* displays the eigenvalues and eigenvectors of the          */
   /* matrix of quadratic parameter estimates to determine if   */
   /* the solution is a maximum or minimum, or saddlepoint, and */
   /* which direction has the steepest and gentlest slopes.     */
   /*                                                           */
   /* Given that d contains the factor variables,               */
   /* and y contains the response.                              */
   /*                                                           */
   
   start rsm;
      n=nrow(d);
      k=ncol(d);                                  /* dimensions */
      x=j(n,1,1)||d;                    /* set up design matrix */
      do i=1 to k;
         do j=1 to i;
            x=x||d[,i] #d[,j];
         end;
      end;
      beta=solve(x`*x,x`*y);       /* solve parameter estimates */
      print "Parameter Estimates" , beta;
      c=beta[1];                          /* intercept estimate */
      b=beta[2:(k+1)];                      /* linear estimates */
      a=j(k,k,0);
      L=k+1;                     /* form quadratics into matrix */
      do i=1 to k;
         do j=1 to i;
            L=L+1;
            a[i,j]=beta [L,];
         end;
      end;
      a=(a+a`)*.5;                                /* symmetrize */
      xx=-.5*solve(a,b);            /* solve for critical value */
      print , "Critical Factor Values" , xx;
         /* Compute response at critical value */
      yopt=c + b`*xx + xx`*a*xx;
      print , "Response at Critical Value" yopt;
      call eigen(eval,evec,a);
      print , "Eigenvalues and Eigenvectors", eval, evec;
      if min(eval)>0 then print , "Solution Was a Minimum";
      if max(eval)<0 then print , "Solution Was a Maximum";
   finish rsm;

Running the module with the following sample data produces the following results and Output 9.7.1:

   
    /* Sample Problem with Two Factors */
    d={-1 -1, -1  0, -1  1,
        0 -1,  0  0,  0  1,
        1 -1,  1  0,  1  1};
    y={ 71.7, 75.2, 76.3, 79.2, 81.5, 80.2, 80.1, 79.1, 75.8};
    run rsm;