Wavelet Analysis

Reconstructing the Signal from the Wavelet Decomposition

You can use the WAVIFT subroutine to invert a wavelet transformation computed with the WAVFT subroutine. If no thresholding is specified, then up to numerical rounding error this inversion is exact. The following statements provide an illustration of this:

  
       call wavift(reconstructedAbsorbance,decomp); 
       errorSS=ssq(absorbance-reconstructedAbsorbance); 
       print "The reconstruction error sum of squares = " errorSS;
 

The output is shown in Figure 16.15.

ERRORSS The reconstruction error sum of squares = 1.321E-16

Figure 16.15: Exact Reconstruction Property of WAVIFT

Usually you use the WAVIFT subroutine with thresholding specified. This yields a smoothed reconstruction of the input data. You can use the following statements to create a smoothed reconstruction of absorbance and add this variable to the QuartzInfraredSpectrum data set.

  
       call wavift(smoothedAbsorbance,decomp,&SureShrink); 
       create temp from smoothedAbsorbance[colname='smoothedAbsorbance']; 
          append from smoothedAbsorbance; 
       close temp; 
    quit; 
  
    data quartzInfraredSpectrum; 
      set quartzInfraredSpectrum; 
      set temp; 
    run;
 

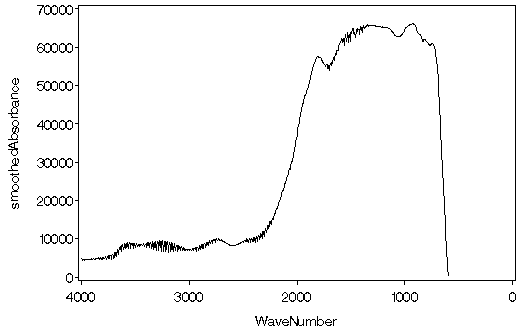
The following statements produce the line plot of the smoothed absorbance data shown in Figure 16.16:

  
    symbol1 c=black i=join v=none; 
    proc gplot data=quartzInfraredSpectrum; 
       plot smoothedAbsorbance*WaveNumber/ 
            hminor = 0   vminor = 0 
            vaxis  = axis1 
            hreverse frame; 
            axis1 label = ( r=0 a=90 ); 
    run;
 

Figure 16.16: Smoothed FT-IR Spectrum of Quartz

You can see by comparing Figure 16.1 with Figure 16.16 that the wavelet smooth of the absorbance data has preserved all the essential features of these data.