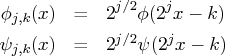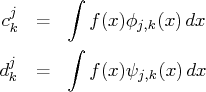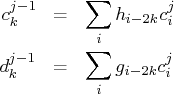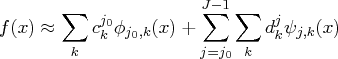: Some Brief Mathematical Preliminaries :: SAS/IML(R) 9.2 User's Guide

Wavelet Analysis

Some Brief Mathematical Preliminaries

The discrete wavelet transform decomposes a function as a sum of basis functions called wavelets. These basis functions have the property that they can be obtained by dilating and translating two basic types of wavelets known as the scaling function, or father wavelet $\phi$ , and the mother wavelet $\psi$ . These translations and dilations are defined as follows:

$\phi_{j,k}(x) & = & 2^{j/2} \phi( 2^j x - k) \ \psi_{j,k}(x) & = & 2^{j/2} \psi( 2^j x - k) \$

The index

defines the dilation or level while the index

defines the translate. Loosely speaking, sums of the $\phi_{j,k}(x)$ capture low frequencies and sums of the $\psi_{j,k}(x)$ represent high frequencies in the data. More precisely, for any suitable function

and for any

$f(x)= \sum_k c^{j_0}_k \phi_{j_0,k}(x) + \sum_{j \geq j_0} \sum_k d^j_k \psi_{j,k}(x)$

where the

and

are known as the scaling coefficients and the detail coefficients, respectively. For orthonormal wavelet families these coefficients can be computed by

$c^j_k & = & \int f(x) \phi_{j,k}(x) \,dx \ d^j_k & = & \int f(x) \psi_{j,k}(x) \,dx$

The key to obtaining fast numerical algorithms for computing the detail and scaling coefficients for a given function

is that there are simple recurrence relationships that enable you to compute the coefficients at level

from the values of the scaling coefficients at level

. These formulas are

$c^{j-1}_k & = & \sum_i h_{i-2k} c^j_i \ d^{j-1}_k & = & \sum_i g_{i-2k} c^j_i$

The coefficients

and

that appear in these formulas are called filter coefficients. The

are determined by the father wavelet and they form a low-pass filter; $g_k=(-1)^k h_{1-k}$ and form a high-pass filter. The preceding sums are formally over the entire (infinite) range of integers. However, for wavelets that are zero except on a finite interval, only finitely many of the filter coefficients are nonzero, and so in this case the sums in the recurrence relationships for the detail and scaling coefficients are finite.

Conversely, if you know the detail and scaling coefficients at level , then you can obtain the scaling coefficients at level by using the relationship

$c^j_k = \sum_i h_{k-2i} c^{j-1}_i + \sum_i g_{k-2i}d^{j-1}_i$

Suppose that you have data values

at equally spaced points . It turns out that the values $2^{-j/2} y_k$ are good approximations of the scaling coefficients . Then, by using the recurrence formula, you can find $c^{j-1}_k$ and $d^{j-1}_k$ , . The discrete wavelet transform of the at level consists of the scaling and detail coefficients at level . A technical point that arises is that in applying the recurrence relationships to finite data, a few values of the for $k\lt$ or $k\geq n$ might be needed. One way to cope with this difficulty is to extend the sequence to the left and right by using some specified boundary treatment.

Continuing by replacing the scaling coefficients at any level by the scaling and detail coefficients at level yields a sequence of coefficients

$\{c^0_0,d^0_0,d^1_0,d^1_1,d^2_0,d^2_1,d^2_2,d^2_3,d^3_1, ... ,d^3_7, ... ,d^{j-1}_0, ... ,d^{j-1}_{n/2-1}\}$

This sequence is the finite discrete wavelet transform of the input data $\{y_k\}$ . At any level the finite dimensional approximation of the function is

$f(x)\approx \sum_k c^{j_0}_k \phi_{j_0,k}(x) + \sum_{j=j_0}^{j-1} \sum_k d^j_k \psi_{j,k}(x)$

Top of Page