| Tutorial: A Module for Linear Regression |
Solving a System of Equations
Because IML is built around traditional matrix algebra notation, it is often possible to directly translate mathematical methods from matrix algebraic expressions into executable IML statements. For example, consider the problem of solving three simultaneous equations:
> proc iml;
IML Ready
Enter this statement:
> reset print;
The PRINT option of the RESET command
causes automatic printing of results.
Notice that as you submit each statement,
it is executed and the results are displayed.
While you are learning IML or developing modules, it is
a good idea to have all results printed automatically.
When you are familiar with SAS/IML software,
you will not need to use automatic printing.
Next, set up the matrices ![]() and
and ![]() .
Both of these matrices are input as matrix literals;
that is, input the row and column values as discussed in
Chapter 2.
.
Both of these matrices are input as matrix literals;
that is, input the row and column values as discussed in
Chapter 2.
> a={3 -1 2,
> 2 -2 3,
> 4 1 -4};
A 3 rows 3 cols (numeric)
3 -1 2
2 -2 3
4 1 -4
> c={8, 2, 9};
C 3 rows 1 col (numeric)
8
2
9
Now write the solution equation,
![]() , as an IML statement, as follows.
The appropriate statement is an assignment statement
that uses a built-in function and an operator (INV is
a built-in function that takes the inverse of a square
matrix, and * is the operator for matrix multiplication).
, as an IML statement, as follows.
The appropriate statement is an assignment statement
that uses a built-in function and an operator (INV is
a built-in function that takes the inverse of a square
matrix, and * is the operator for matrix multiplication).
> x=inv(a)*c;
X 3 rows 1 col (numeric)
3
5
2
After IML executes the statement, the first row of matrix
![]() contains the
contains the ![]() value for which you
are solving, the second row contains the
value for which you
are solving, the second row contains the ![]() value, and the third row contains the
value, and the third row contains the ![]() value.
value.
Now end the session by entering the QUIT command:
> quit;
Exiting IML
Copyright © 2009 by SAS Institute Inc., Cary, NC, USA. All rights reserved.
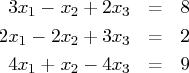
![[ 3 & -1 & 2 \ 2 & -2 & 3 \ 4 & 1 & -4 \ ] [ x_1 \ x_2 \ x_3 \ ] = [ 8 \ 2 \ 9 \ ]](images/tutorial_tutorialeq3.gif)