Time Series Analysis and Examples: Getting Started

Time Series Analysis and Examples

Getting Started

The fractional differencing enables the degree of differencing to take any real value rather than being restricted to integer values. The fractionally differenced processes are capable of modeling long-term persistence. The process

$(1-b)^dy_{t} = {\epsilon}_t$

is known as a fractional Gaussian noise process or an ARFIMA(

) process, where $d\in (-1,1) \backslash \{0\}$ , $\epsilon_t$ is a white noise process with mean zero and variance $\sigma_{\epsilon}^2$ , and

is the backshift operator such that $b^j{y}_{t}=y_{t-j}$ . The extension of an ARFIMA(

) model combines fractional differencing with an ARMA(

) model, known as an ARFIMA(

) model.

Consider an ARFIMA() represented as $(1-b)^{0.4}y_{t} = {\epsilon}_t$ where $\epsilon_t \sim iid n(0, 2)$ . With the following statements you can

generate the simulated 300 observations data
obtain the fractionally differenced data
compute the autocovariance function
compute the log-likelihood function
fit a fractionally integrated time series model to the data

  
    proc iml; 
       /* ARFIMA(0,0.4,0) */ 
       lag = (0:12)`; 
       call farmacov(autocov_D_IS_04, 0.4); 
       call farmacov(D_IS_005, 0.05); 
       print lag autocov_D_IS_04 D_IS_005; 
       d = 0.4; 
       call farmasim(yt, d) n = 300 sigma = 2 seed=5345; print yt; 
       call fdif(zt, yt, d); print zt; 
       call farmalik(lnl, yt, d); print lnl; 
       call farmafit(d, ar, ma, sigma, yt); print d sigma;

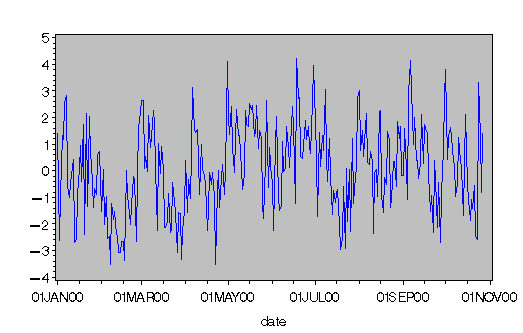
$fractg01.gif (8760 bytes)$

Figure 10.34: Plot of Generated ARFIMA(0,0.4,0) Process (FARMASIM)

The FARMASIM function generates the data shown in Figure 10.34.

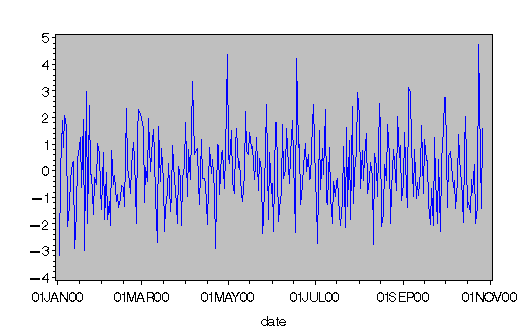
$fractg02.gif (9118 bytes)$

Figure 10.35: Plot of Fractionally Differenced Process (FDIF)

The FDIF function creates the fractionally differenced process. Figure 10.35 shows a white noise series.

LAG	AUTOCOV_D_IS_04	D_IS_005
0	2.0700983	1.0044485
1	1.3800656	0.0528657
2	1.2075574	0.0284662
3	1.1146683	0.0197816
4	1.0527423	0.0152744
5	1.0069709	0.0124972
6	0.9710077	0.0106069
7	0.9415832	0.0092333
8	0.9168047	0.008188
9	0.8954836	0.0073647
10	0.8768277	0.0066985
11	0.8602838	0.006148
12	0.8454513	0.0056849

Figure 10.36: Autocovariance Functions of ARFIMA(0,0.4,0) and ARFIMA(0,0.05,0) Models (FARMACOV)

The first column is the autocovariance function of the ARFIMA(0,0.4,0) model, and the second column is the autocovariance function of the ARFIMA(0,0.05,0) model. The first column decays to zero more slowly than the second column.

LNL
-101.2222
.
.

Figure 10.37: Log-Likelihood Function of ARFIMA(0,0.4,0) Model (FARMALIK)

The first row value is the log-likelihood function of the ARFIMA(0,0.4,0) model. Since the default option of the estimates method is the conditional sum of squares, the last two rows of Figure 10.37 do not have the values since the default estimation method is used.

D	SIGMA
0.386507	1.9631754

Figure 10.38: Parameter Estimation of ARFIMA(0,0.4,0) Model (FARMAFIT)

The final estimates of the parameters are and $\sigma^2=1.96$ , while the true values of the data generating process are and $\sigma^2=2$ .

Top of Page