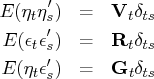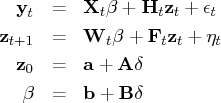| Time Series Analysis and Examples |
Getting Started
The measurement (or observation) equation can be written
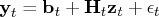
where
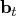
is an
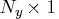
vector,
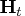
is an
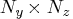
matrix, the sequence of observation noise
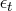
is independent,
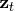
is an
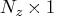
state vector, and
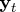
is an
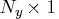
observed vector.
The transition (or state) equation is denoted as
a first-order Markov process of the state vector.
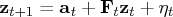
where
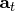
is an
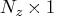
vector,
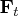
is an
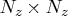
transition matrix, and the
sequence of transition noise
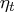
is independent.
This equation is often called a
shifted transition equation
because the state vector is shifted forward one time period.
The transition equation can also be
denoted by using an alternative specification
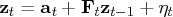
There is no real difference between the shifted transition
equation and this alternative equation if the observation
noise and transition equation noise are uncorrelated -
that is,
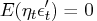
.
It is assumed that
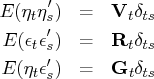
where
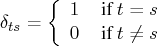
De Jong (1991a) proposed a diffuse Kalman filter that can
handle an arbitrarily large initial state covariance matrix.
The diffuse initial state assumption is
reasonable if you encounter the case of
parameter uncertainty or SSM nonstationarity.
The SSM of the diffuse Kalman filter is written
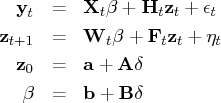
where
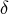
is a random variable with a mean
of
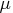
and a variance of
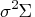
.
When
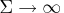
, the SSM is said to be diffuse.
The KALCVF call computes the one-step prediction
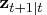 and the filtered estimate
and the filtered estimate 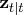 ,
together with their covariance matrices
,
together with their covariance matrices 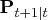 and
and 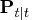 , using forward recursions.
You can obtain the
, using forward recursions.
You can obtain the 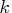 -step prediction
-step prediction 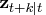 and
its covariance matrix
and
its covariance matrix 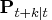 with the KALCVF call.
The KALCVS call uses backward recursions to compute the smoothed
estimate
with the KALCVF call.
The KALCVS call uses backward recursions to compute the smoothed
estimate 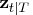 and its covariance matrix
and its covariance matrix 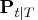 when there are
when there are 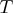 observations in the complete data.
observations in the complete data.
The KALDFF call produces one-step prediction
of the state and the unobserved random vector
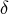 as well as their covariance matrices.
The KALDFS call computes the smoothed estimate
as well as their covariance matrices.
The KALDFS call computes the smoothed estimate
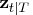 and its covariance matrix
and its covariance matrix 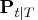 .
.
Copyright © 2009 by SAS Institute Inc., Cary, NC, USA. All rights reserved.
![]() and the filtered estimate
and the filtered estimate ![]() ,
together with their covariance matrices
,
together with their covariance matrices ![]() and
and ![]() , using forward recursions.
You can obtain the
, using forward recursions.
You can obtain the ![]() -step prediction
-step prediction ![]() and
its covariance matrix
and
its covariance matrix ![]() with the KALCVF call.
The KALCVS call uses backward recursions to compute the smoothed
estimate
with the KALCVF call.
The KALCVS call uses backward recursions to compute the smoothed
estimate ![]() and its covariance matrix
and its covariance matrix ![]() when there are
when there are ![]() observations in the complete data.
observations in the complete data.
![]() as well as their covariance matrices.
The KALDFS call computes the smoothed estimate
as well as their covariance matrices.
The KALDFS call computes the smoothed estimate
![]() and its covariance matrix
and its covariance matrix ![]() .
.