| Time Series Analysis and Examples |
Example 10.1: VAR Estimation and Variance Decomposition
In this example, a VAR model is estimated and forecast. The VAR(3) model is estimated by using investment, durable consumption, and consumption expenditures. The data are found in the appendix to Lütkepohl (1993). The stationary VAR(3) process is specified as
The matrix ARCOEF contains the AR coefficients
(![]() ,
,![]() , and
, and ![]() ), and the matrix EV contains
error covariance estimates. An intercept vector
), and the matrix EV contains
error covariance estimates. An intercept vector ![]() is
included in the first row of the matrix ARCOEF if OPT[1]=1
is specified. Here is the code:
is
included in the first row of the matrix ARCOEF if OPT[1]=1
is specified. Here is the code:
data one;
input invest income consum @@;
datalines;
180 451 415 179 465 421 185 485 434 192 493 448
211 509 459 202 520 458 207 521 479 214 540 487
231 548 497 229 558 510 234 574 516 237 583 525
206 591 529 250 599 538 259 610 546 263 627 555
264 642 574 280 653 574 282 660 586 292 694 602
286 709 617 302 734 639 304 751 653 307 763 668
317 766 679 314 779 686 306 808 697 304 785 688
292 794 704 275 799 699 273 799 709 301 812 715
280 837 724 289 853 746 303 876 758 322 897 779
315 922 798 339 949 816 364 979 837 371 988 858
375 1025 881 432 1063 905 453 1104 934 460 1131 968
475 1137 983 496 1178 1013 494 1211 1034 498 1256 1064
526 1290 1101 519 1314 1102 516 1346 1145 531 1385 1173
573 1416 1216 551 1436 1229 538 1462 1242 532 1493 1267
558 1516 1295 524 1557 1317 525 1613 1355 519 1642 1371
526 1690 1402 510 1759 1452 519 1756 1485 538 1780 1516
549 1807 1549 570 1831 1567 559 1873 1588 584 1897 1631
611 1910 1650 597 1943 1685 603 1976 1722 619 2018 1752
635 2040 1774 658 2070 1807 675 2121 1831 700 2132 1842
692 2199 1890 759 2253 1958 782 2276 1948 816 2318 1994
844 2369 2061 830 2423 2056 853 2457 2102 852 2470 2121
833 2521 2145 860 2545 2164 870 2580 2206 830 2620 2225
801 2639 2235 824 2618 2237 831 2628 2250 830 2651 2271
;
proc iml;
use one;
read all into y var{invest income consum};
mdel = 1;
maice = 0;
misw = 0; /*-- instantaneous modeling ? --*/
call tsmulmar(arcoef,ev,nar,aic) data=y maxlag=3
opt=(mdel || maice || misw) print=1;
To obtain the unit triangular matrix ![]() and
diagonal matrix
and
diagonal matrix ![]() , you need to estimate the
instantaneous
response model. When you specify the OPT[3]=1 option, the
first row of the output matrix EV contains error variances of
the instantaneous response model, while the unit
triangular matrix is in the second through the fifth rows.
See Output 10.1.1. Here is the code:
, you need to estimate the
instantaneous
response model. When you specify the OPT[3]=1 option, the
first row of the output matrix EV contains error variances of
the instantaneous response model, while the unit
triangular matrix is in the second through the fifth rows.
See Output 10.1.1. Here is the code:
misw = 1;
call tsmulmar(arcoef,ev,nar,aic) data=y maxlag=3
opt=(mdel || maice || misw) print=1;
print ev;
Output 10.1.1: Error Variance and Unit Triangular Matrix
|
|
| EV | ||
| 295.21042 | 190.94664 | 59.361516 |
| 1 | 0 | 0 |
| -0.02239 | 1 | 0 |
| -0.256341 | -0.500803 | 1 |
In Output 10.1.2 and Output 10.1.3, you can see the relationship
between the instantaneous response model and the VAR model.
The VAR coefficients are computed as ![]() ,
where
,
where ![]() is a coefficient matrix of the instantaneous model.
For example, you can verify this result by using the first lag
coefficient matrix
is a coefficient matrix of the instantaneous model.
For example, you can verify this result by using the first lag
coefficient matrix ![]() .
.
Output 10.1.3: Instantaneous Response Model Estimates
| ||||||||||||||||||||||||||||||
When the VAR estimates are available, you can forecast
the future values by using the TSPRED call. As a
default, the one-step predictions are produced until
the START= point is reached. The NPRED=![]() option
specifies how far you want to predict. The prediction
error covariance matrix MSE contains
option
specifies how far you want to predict. The prediction
error covariance matrix MSE contains ![]() mean
square error matrices. The output matrix IMPULSE contains
the estimate of the coefficients
mean
square error matrices. The output matrix IMPULSE contains
the estimate of the coefficients ![]() of the
infinite MA process. The following IML code estimates
the VAR(3) model and performs 10-step-ahead prediction.
of the
infinite MA process. The following IML code estimates
the VAR(3) model and performs 10-step-ahead prediction.
mdel = 1;
maice = 0;
misw = 0;
call tsmulmar(arcoef,ev,nar,aic) data=y maxlag=3
opt=(mdel || maice || misw);
call tspred(forecast,impulse,mse,y,arcoef,nar,0,ev)
npred=10 start=nrow(y) constant=mdel;
print impulse;
The lagged effects of a unit increase in the error disturbances are included in the matrix IMPULSE. For example:
| ||||||||||||||||||||||||||||||||||||||||||||||||
In addition, you can compute the lagged response on the one-unit
increase in the orthogonalized disturbances
![]() .
.
When the error matrix EV is obtained from the instantaneous
response model, you need to convert the matrix IMPULSE.
The first 15 rows of the matrix ORTH_IMP are shown in
Output 10.1.5. Note that the matrix constructed from the last three
rows of EV become the matrix ![]() . Here is the code:
. Here is the code:
call tsmulmar(arcoef,ev,nar,aic) data=y maxlag=3
opt={1 0 1};
lmtx = inv(ev[2:nrow(ev),]);
orth_imp = impulse * lmtx;
print orth_imp;
Output 10.1.5: Transformed Moving-Average Coefficients
| ||||||||||||||||||||||||||||||||||||||||||||||||
You can verify the result for the case of
The contribution of the ![]() th orthogonalized
innovation to the mean square error matrix of the 10-step forecast
is computed by using the formula
th orthogonalized
innovation to the mean square error matrix of the 10-step forecast
is computed by using the formula
In Output 10.1.6, diagonal elements of each decomposed MSE matrix are displayed as the matrix CONTRIB as well as those of the MSE matrix (VAR). Here is the code:
mse1 = j(3,3,0);
mse2 = j(3,3,0);
mse3 = j(3,3,0);
do i = 1 to 10;
psi = impulse[(i-1)*3+1:3*i,];
mse1 = mse1 + psi*lmtx[,1]*lmtx[,1]`*psi`;
mse2 = mse2 + psi*lmtx[,2]*lmtx[,2]`*psi`;
mse3 = mse3 + psi*lmtx[,3]*lmtx[,3]`*psi`;
end;
mse1 = ev[1,1]#mse1;
mse2 = ev[1,2]#mse2;
mse3 = ev[1,3]#mse3;
contrib = vecdiag(mse1) || vecdiag(mse2) || vecdiag(mse3);
var = vecdiag(mse[28:30,]);
print contrib var;
Output 10.1.6: Orthogonal Innovation Contribution
| ||||||||||||||||
The investment innovation contribution to its own variable
is 1879.3774, and the income innovation contribution to
the consumption expenditure is 1916.1676. It is easy to understand
the contribution of innovations in the ![]() th variable to MSE
when you compute the innovation account. In Output 10.1.7,
innovations in the first variable (investment) explain 20.45%
of the error variance of the second variable (income), while the
innovations in the second variable explain 79.5% of its own
error variance. It is straightforward to construct the general
multistep forecast error variance decomposition. Here is the code:
th variable to MSE
when you compute the innovation account. In Output 10.1.7,
innovations in the first variable (investment) explain 20.45%
of the error variance of the second variable (income), while the
innovations in the second variable explain 79.5% of its own
error variance. It is straightforward to construct the general
multistep forecast error variance decomposition. Here is the code:
account = contrib * 100 / (var@j(1,3,1));
print account;
Output 10.1.7: Innovation Account
| ||||||||||||
Copyright © 2009 by SAS Institute Inc., Cary, NC, USA. All rights reserved.
![\hspace*{-.9in} [0.886 & 0.340 & -0.014 \ 0.168 & 1.050 & 0.107 \ 0.089 & ... ....886 & 0.340 & -0.014 \ 0.149 & 1.043 & 0.107 \ -0.222 & -0.154 & 0.397 ]](images/timeseriesexpls_timeseriesexplseq381.gif)
![\frac{\partial{y}_{t+2}}{\partial\epsilon^'_t} = [0.781100 & 0.353140 & 0.180211 \ 0.448501 & 1.165474 & 0.069731 \ 0.364611 & 0.692111 & 0.222342 ]](images/timeseriesexpls_timeseriesexplseq384.gif)
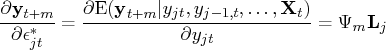
![[0.443390 \ 1.200395 \ 0.803461 ] = [0.781100 & 0.353140 & 0.180211 \ 0.44... ...31 \ 0.364611 & 0.692111 & 0.222342 ] [0.000000 \ 1.000000 \ 0.500803 ]](images/timeseriesexpls_timeseriesexplseq387.gif)