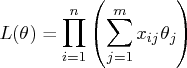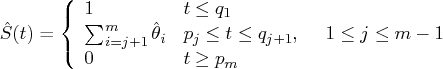Nonlinear Optimization Examples: Example 11.6: Survival Curve for Interval Censored Data

Nonlinear Optimization Examples

Example 11.6: Survival Curve for Interval Censored Data

In some studies, subjects are assessed only periodically for outcomes or responses of interest. In such situations, the occurrence times of these events are not observed directly; instead they are known to have occurred within some time interval. The times of occurrence of these events are said to be interval censored. A first step in the analysis of these interval censored data is the estimation of the distribution of the event occurrence times.

In a study with subjects, denote the raw interval censored observations by $\{(l_i,r_i]: 1 \leq i \leq n\}$ . For the th subject, the event occurrence time lies in , where is the last assessment time at which there was no evidence of the event, and is the earliest time when a positive assessment was noted (if it was observed at all). If the event does not occur before the end of the study, is given a value larger than any assessment time recorded in the data.

A set of nonoverlapping time intervals $i_j=(q_j,p_j], \;1 \leq j \leq m$ , is generated over which the survival curve $s(t) = {\rm pr}[t \gt t]$ is estimated. Refer to Peto (1973) and Turnbull (1976) for details. Assuming the independence of and , and also independence across subjects, the likelihood of the data $\{t_i \in (l_i,r_i], 1 \leq i \leq n\}$ can be constructed in terms of the pseudo-parameters $\theta_j = \pr[t_i \in i_j], 1 \leq i \leq m$ . The conditional likelihood of ${\theta}=(\theta_1, ... , \theta_m)$ is

$l(\theta) = \prod_{i=1}^n ( \sum_{j=1}^m x_{ij} \theta_j )$

where $x_{ij}$ is 1 or 0 according to whether

is a subset of

. The maximum likelihood estimates, $\hat{\theta}_j,1 \leq j \leq m$ , yield an estimator $\hat{s}(t)$ of the survival function

, which is given by

$\hat{s}(t) = \{ 1 & t \leq q_1 \ \sum_{i=j+1}^m \hat{\theta}_i & p_j \leq t \leq q_{j+1}, 1\leq j\leq {m-1} \ 0 & t \geq p_m .$

$\hat{s}(t)$ remains undefined in the intervals where the function can decrease in an arbitrary way. The asymptotic covariance matrix of $\hat{\theta}$ is obtained by inverting the estimated matrix of second partial derivatives of the negative log likelihood (Peto 1973, Turnbull 1976). You can then compute the standard errors of the survival function estimators by the delta method and approximate the confidence intervals for survival function by using normal distribution theory.

The following code estimates the survival curve for interval censored data. As an illustration, consider an experiment to study the onset of a special kind of palpable tumor in mice. Forty mice exposed to a carcinogen were palpated for the tumor every two weeks. The times to the onset of the tumor are interval censored data. These data are contained in the data set CARCIN. The variable L represents the last time the tumor was not yet detected, and the variable R represents the first time the tumor was palpated. Three mice died tumor free, and one mouse was tumor free by the end of the 48-week experiment. The times to tumor for these four mice were considered right censored, and they were given an R value of 50 weeks.

  
    data carcin; 
       input id l r @@; 
       datalines; 
       1  20  22    11  30  32     21  22  24    31  34  36 
       2  22  24    12  32  34     22  22  24    32  34  36 
       3  26  28    13  32  34     23  28  30    33  36  38 
       4  26  28    14  32  34     24  28  30    34  38  40 
       5  26  28    15  34  36     25  32  34    35  38  40 
       6  26  28    16  36  38     26  32  34    36  42  44 
       7  28  30    17  42  44     27  32  34    37  42  44 
       8  28  30    18  30  50     28  32  34    38  46  48 
       9  30  32    19  34  50     29  32  34    39  28  50 
      10  30  32    20  20  22     30  32  34    40  48  50 
       ; 
  
    proc iml; 
       use carcin; 
       read all var{l r}; 
       nobs= nrow(l); 
      /********************************************************* 
          construct the nonoverlapping intervals (Q,P) and 
          determine the number of pseudo-parameters (NPARM) 
       *********************************************************/ 
       pp= unique(r); npp= ncol(pp); 
       qq= unique(l); nqq= ncol(qq); 
       q= j(1,npp, .); 
       do; 
          do i= 1 to npp; 
             do j= 1 to nqq; 
                if ( qq[j] < pp[i] ) then q[i]= qq[j]; 
             end; 
             if q[i] = qq[nqq] then goto lab1; 
          end; 
       lab1: 
       end; 
  
       if i > npp then nq= npp; 
       else            nq= i; 
       q= unique(q[1:nq]); 
       nparm= ncol(q); 
       p= j(1,nparm, .); 
       do i= 1 to nparm; 
          do j= npp to 1 by -1; 
             if ( pp[j] > q[i] ) then p[i]= pp[j]; 
          end; 
       end; 
  
      /******************************************************** 
          generate the X-matrix for the likelihood 
       ********************************************************/ 
       _x= j(nobs, nparm, 0); 
       do j= 1 to nparm; 
          _x[,j]= choose(l <= q[j]  & p[j] <= r, 1, 0); 
       end; 
  
      /******************************************************** 
         log-likelihood function (LL) 
       ********************************************************/ 
       start LL(theta) global(_x,nparm); 
          xlt= log(_x * theta`); 
          f= xlt[+]; 
          return(f); 
       finish LL; 
  
      /******************************************************** 
         gradient vector (GRAD) 
       *******************************************************/ 
       start GRAD(theta) global(_x,nparm); 
          g= j(1,nparm,0); 
          tmp= _x # (1 /  (_x * theta`) ); 
          g= tmp[+,]; 
          return(g); 
       finish GRAD; 
  
      /************************************************************* 
         estimate the pseudo-parameters using quasi-newton technique 
       *************************************************************/ 
       /* options */ 
       optn= {1 2}; 
  
       /* constraints */ 
       con= j(3, nparm + 2, .); 
       con[1, 1:nparm]= 1.e-6; 
       con[2:3, 1:nparm]= 1; 
       con[3,nparm + 1]=0; 
       con[3,nparm + 2]=1; 
  
       /* initial estimates */ 
       x0= j(1, nparm, 1/nparm); 
  
       /* call the optimization routine */ 
       call nlpqn(rc,rx,"LL",x0,optn,con,,,,"GRAD"); 
  
      /************************************************************* 
        survival function estimate (SDF) 
       ************************************************************/ 
       tmp1= cusum(rx[nparm:1]); 
       sdf= tmp1[nparm-1:1]; 
  
  
      /************************************************************* 
        covariance matrix of the first nparm-1 pseudo-parameters (SIGMA2) 
       *************************************************************/ 
       mm= nparm - 1; 
       _x= _x - _x[,nparm] * (j(1, mm, 1) || {0}); 
       h= j(mm, mm, 0); 
       ixtheta= 1 / (_x * ((rx[,1:mm]) || {1})`); 
       if _zfreq then 
          do i= 1 to nobs; 
             rowtmp= ixtheta[i] # _x[i,1:mm]; 
             h= h + (_freq[i] # (rowtmp` * rowtmp)); 
          end; 
       else do i= 1 to nobs; 
          rowtmp= ixtheta[i] # _x[i,1:mm]; 
          h= h + (rowtmp` * rowtmp); 
       end; 
       sigma2= inv(h); 
  
      /************************************************************* 
        standard errors of the estimated survival curve (SIGMA3) 
       *************************************************************/ 
       sigma3= j(mm, 1, 0); 
       tmp1= sigma3; 
       do i= 1 to mm; 
          tmp1[i]= 1; 
          sigma3[i]= sqrt(tmp1` * sigma2 * tmp1); 
       end; 
  
      /************************************************************* 
        95% confidence limits for the survival curve (LCL,UCL) 
       *************************************************************/ 
      /* confidence limits */ 
       tmp1= probit(.975); 
       *print tmp1; 
       tmp1= tmp1 * sigma3; 
       lcl= choose(sdf > tmp1, sdf - tmp1, 0); 
       ucl= sdf + tmp1; 
       ucl= choose( ucl > 1., 1., ucl); 
  
      /************************************************************* 
        print estimates of pseudo-parameters 
       *************************************************************/ 
       reset center noname; 
       q= q`; 
       p= p`; 
       theta= rx`; 
       print ,"Parameter Estimates", ,q[colname={q}] p[colname={p}] 
             theta[colname={theta} format=12.7],; 
  
      /************************************************************* 
        print survival curve estimates and confidence limits 
       *************************************************************/ 
       left= {0} // p; 
       right= q // p[nparm]; 
       sdf= {1} // sdf // {0}; 
       lcl= {.} // lcl //{.}; 
       ucl= {.} // ucl //{.}; 
       print , "Survival Curve Estimates and 95% Confidence Intervals", , 
             left[colname={left}] right[colname={right}] 
             sdf[colname={estimate} format=12.4] 
             lcl[colname={lower} format=12.4] 
             ucl[colname={upper} format=12.4];

The iteration history produced by the NLPQN subroutine is shown in Output 11.6.1.

Output 11.6.1: Iteration History for the NLPQN Subroutine

Dual Quasi-Newton Optimization

Dual Broyden - Fletcher - Goldfarb - Shanno Update (DBFGS)

Parameter Estimates	12
Lower Bounds	12
Upper Bounds	12
Linear Constraints	1

Optimization Start
Active Constraints	1	Objective Function	-93.3278404
Max Abs Gradient Element	65.361558529

Iteration	Restarts	Function Calls	Active Constraints	Objective Function	Objective Function Change	Max Abs Gradient Element	Step Size	Slope of Search Direction
1	0	3	1	-88.51201	4.8158	16.6594	0.0256	-305.2
2	0	4	1	-87.42665	1.0854	10.8769	1.000	-2.157
3	0	5	1	-87.27408	0.1526	5.4965	1.000	-0.366
4	0	7	1	-87.17314	0.1009	2.2856	2.000	-0.113
5	0	8	1	-87.16611	0.00703	0.3444	1.000	-0.0149
6	0	10	1	-87.16582	0.000287	0.0522	1.001	-0.0006
7	0	12	1	-87.16581	9.128E-6	0.00691	1.133	-161E-7
8	0	14	1	-87.16581	1.712E-7	0.00101	1.128	-303E-9

Optimization Results
Iterations	8	Function Calls	15
Gradient Calls	11	Active Constraints	1
Objective Function	-87.16581343	Max Abs Gradient Element	0.0010060788
Slope of Search Direction	-3.033154E-7

GCONV convergence criterion satisfied.

NOTE:

At least one element of the (projected) gradient is greater than 1e-3.

The estimates of the pseudo-parameter for the nonoverlapping intervals are shown in Output 11.6.2.

Output 11.6.2: Estimates for the Probability of Event Occurrence

Q	P	THETA
20	22	0.0499997
22	24	0.0749988
26	28	0.0999978
28	30	0.1033349
30	32	0.0806014
32	34	0.2418023
34	36	0.0873152
36	38	0.0582119
38	40	0.0582119
42	44	0.0873152
46	48	0.0291055
48	50	0.0291055

The survival curve estimates and confidence intervals are displayed in Output 11.6.3.

Output 11.6.3: Survival Estimates and Confidence Intervals

LEFT	RIGHT	ESTIMATE	LOWER	UPPER
0	20	1.0000	.	.
22	22	0.9500	0.8825	1.0000
24	26	0.8750	0.7725	0.9775
28	28	0.7750	0.6456	0.9044
30	30	0.6717	0.5252	0.8182
32	32	0.5911	0.4363	0.7458
34	34	0.3493	0.1973	0.5013
36	36	0.2619	0.1194	0.4045
38	38	0.2037	0.0720	0.3355
40	42	0.1455	0.0293	0.2617
44	46	0.0582	0.0000	0.1361
48	48	0.0291	0.0000	0.0852
50	50	0.0000	.	.

In this program, the quasi-Newton technique is used to maximize the likelihood function. You can replace the quasi-Newton routine by other optimization routines, such as the NLPNRR subroutine, which performs Newton-Raphson ridge optimization, or the NLPCG subroutine, which performs conjugate gradient optimization. Depending on the number of parameters and the number of observations, these optimization routines do not perform equally well. For survival curve estimation, the quasi-Newton technique seems to work fairly well since the number of parameters to be estimated is usually not too large.

Top of Page