| Module Library |
RANDWISHART Function
generates a random sample from a Wishart distribution
- RANDWISHART( N, DF, Sigma )
The inputs are as follows:
- is the number of desired observations sampled from the distribution.
- DF
- is a scalar value representing the degrees of
freedom,
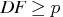 .
.
- Sigma
- is a
 symmetric positive definite
matrix.
symmetric positive definite
matrix.
The RANDWISHART function returns an
The Wishart distribution is a multivariate generalization of the gamma distribution. (Note, however, that Kotz, Balakrishnan, and Johnson 2000 suggest that the term "multivariate gamma distribution" should be restricted to those distributions for which the marginal distributions are univariate gamma. This is not the case with the Wishart distribution.) A Wishart distribution is a probability distribution for nonnegative definite matrix-valued random variables. These distributions are often used to estimate covariance matrices.
If a
- the probability density function for
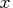 is
is
- if
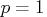 and
and 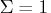 , then the Wishart distribution
reduces to a chi-square distribution
with
, then the Wishart distribution
reduces to a chi-square distribution
with 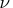 degrees of freedom.
degrees of freedom.
- the expected value of
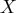 is
is 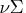 .
.
The following example generates 1000 samples from a Wishart
distribution with 7 degrees of freedom and ![]() matrix
parameter S. Each row of the returned matrix x represents
a
matrix
parameter S. Each row of the returned matrix x represents
a ![]() nonnegative definite matrix. (You can reshape the
nonnegative definite matrix. (You can reshape the ![]() th
row of x with the SHAPE function.) The example then computes
the sample mean and compares them with the expected value. Here are
the code and the output:
th
row of x with the SHAPE function.) The example then computes
the sample mean and compares them with the expected value. Here are
the code and the output:
call randseed(1);
N=1000;
DF = 7;
S = {1 1, 1 5};
x = RandWishart( N, DF, S );
ExpectedValue = DF * S;
SampleMean = shape( x[:,], 2, 2);
print SampleMean ExpectedValue;
SampleMean ExpectedValue
7.0518633 14.103727 7 14
14.103727 28.207453 14 28
For further details about sampling from the Wishart distribution, see Johnson (1987, pp. 203 - 204).
Copyright © 2009 by SAS Institute Inc., Cary, NC, USA. All rights reserved.