Understanding the Interactive Matrix Language

Assignment Statements

Assignment statements create matrices by evaluating expressions and assigning the results to a matrix. The expressions can be composed of operators (for example, matrix multiplication) or functions (for example, matrix inversion) operating on matrices. Because of the nature of linear algebraic expressions, the resulting matrices automatically acquire appropriate characteristics and values. Assignment statements have the following general form:

where result is the name of the new matrix and expression is an expression that is evaluated, the results of which are assigned to the new matrix.

Functions as Expressions

Matrices can be created as a result of a function call. Scalar functions such as LOG or SQRT operate on each element of a matrix, while matrix functions such as INV or RANK operate on the entire matrix. For example, the following statement assigns the square root of each element of to the corresponding element of :

  
    a=sqrt(b);
 

The following statement calls the INV function to compute the inverse matrix of and assign the results to :

  
    y=inv(x);
 

The following statement creates a matrix with elements that are the ranks of the corresponding elements of :

  
    r=rank(x);
 

Operators within Expressions

There are three types of operators that can be used in assignment statement expressions. Be sure that the matrices on which an operator acts are conformable to the operation. For example, matrix multiplication requires that the number of columns of the left-hand matrix be equal to the number of rows of the right-hand matrix.

The three types of operators are as follows:

prefix operators

are placed in front of an operand ().

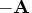infix operators

are placed between operands ().

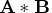postfix operators

are placed after an operand ().

All operators can work in a one-to-many or many-to-one manner; that is, they enable you to, for example, add a scalar to a matrix or divide a matrix by a scalar. The following is an example of using operators in an assignment statement:

  
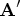    y=x#(x>0);
 

This assignment statement creates a matrix in which each negative element of the matrix is replaced with zero. The statement actually has two expressions evaluated. The expression (>0) is a many-to-one operation that compares each element of to zero and creates a temporary matrix of results; an element of the temporary matrix is 1 when the corresponding element of is positive, and 0 otherwise. The original matrix is then multiplied elementwise by the temporary matrix, resulting in the matrix .

For a complete listing and explanation of operators, see Chapter 20.