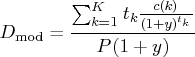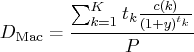Language Reference: DURATION Function :: SAS/IML(R) 9.2 User's Guide

Language Reference

DURATION Function

calculates and returns a scalar containing the modified duration of a noncontingent cash flow.

DURATION( times,flows,ytm)

The DURATION function returns the modified duration of a noncontingent cash flow as a scalar.

times: is an 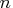-dimensional column vector of times. Elements should be nonnegative.
flows: is an 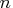-dimensional column vector of cash flows.
ytm: is the per-period yield-to-maturity of the cash-flow stream. This is a scalar and should be positive.

Duration of a security is generally defined as

$d = -\frac{ \frac{dp}p }{ dy }$

In other words, it is the relative change in price for a unit change in yield. Since prices move in the opposite direction to yields, the sign change preserves positivity for convenience. With cash flows that are not yield-sensitive and the assumption of parallel shifts to a flat term structure, duration is given by

$d_{\rm mod}= \frac{ \sum_{k=1}^k t_k \frac{ c(k) } { (1+y)^{t_k} }} { p (1+y) }$

where

is the present value,

is the per-period effective yield-to-maturity,

is the number of cash flows, and the

th cash flow is

periods from the present. This measure is referred to as modified duration to differentiate it from the first duration measure ever proposed, Macaulay duration:

$d_{\rm mac}= \frac{ \sum_{k=1}^k t_k \frac{ c(k) } { (1+y)^{t_k} }} { p }$

This expression also reveals the reason for the name duration, since it is a present-value-weighted average of the duration (that is, timing) of all the cash flows and is hence an ``average time-to-maturity'' of the bond.

For example, consider the following statements:

  
    times={1}; 
    ytm={0.1}; 
    flow={10}; 
    duration=duration(times,flow,ytm); 
    print duration;

These statements produce the following output:

  
    DURATION 
    0.9090909

Top of Page