Language Reference: SPLINE and SPLINEC Calls :: SAS/IML(R) 9.2 User's Guide

Language Reference

SPLINE and SPLINEC Calls

provide cubic spline fits

CALL SPLINE( fitted, data<, smooth<, delta<, nout>

<, type<, slope>);

CALL SPLINEC( fitted, coeff, endSlopes, data<, smooth<, delta>

<, nout<, type<, slope>);

The SPLINE subroutine is the same as SPLINEC but does not return the matrix of spline coefficients needed to call SPLINEV, nor does it return the slopes at the endpoints of the curve.

The SPLINEC subroutine returns the following values:

fitted: is an 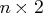matrix of fitted values.
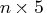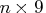coeff: is an (or ) matrix of spline coefficients. The matrix contains the cubic polynomial coefficients for the spline for each interval. Column 1 is the left endpoint of the 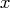-interval for the regular (nonparametric) spline or the left endpoint of the parameter for the parametric spline. Columns 2-5 are the constant, linear, quadratic, and cubic coefficients, respectively, for the -component. 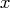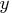If a parametric spline is used, then columns 6-9 are the constant, linear, quadratic, and cubic coefficients, respectively, for the -component. The coefficients for each interval are with respect to the variable where 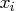is the left endpoint of the interval and 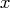is the point of interest. The matrix coeff can be processed to yield the integral or the derivative of the spline. This, in turn, can be used with the SPLINEV function to evaluate the resulting curves. The SPLINEC call returns coeff.
endSlopes: is a matrix containing the slopes of the two ends of the curve expressed as angles in degrees. The SPLINEC call returns the endSlopes argument.

The inputs to the SPLINEC subroutine are as follows:

data

specifies a

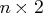(or

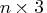) matrix of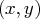

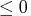points on which the spline is to be fit. The optional third column is used to specify a weight for each data point. If smooth $\gt 0$ , the weight column is used in calculations. A weight $\leq 0$ causes the data point to be ignored in calculations.

smooth

is an optional scalar specifying the degree of smoothing to be used. If smooth is omitted or set equal to 0, then a cubic interpolating spline is fit to the data. If smooth $\gt 0$ , then a cubic spline is used. Larger values of smooth generate more smoothing.

delta

is an optional scalar specifying the resolution constant. If delta is specified, the fitted points are spaced by the amount delta on the scale of the first column of data if a regular spline is used or on the scale of the curve length if a parametric spline is used. If both nout and delta are specified, nout is used and delta is ignored.

nout

is an optional scalar specifying the number of fitted points to be computed. The default is nout=200. If nout is specified, then nout equally spaced points are returned. The nout argument overrides the delta argument.

type

is an optional

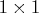(or

) character matrix or quoted literal giving the type of spline to be used. The first element of type should be one of the following:

periodic, which requests periodic endpoints
zero, which sets second derivatives at endpoints to 0

The type argument controls the endpoint constraints unless the slope argument is specified. If periodic is specified, the response values at the beginning and end of column 2 of data must be the same unless the smoothing spline is being used. If the values are not the same, an error message is printed and no spline is fit. The default value is zero. The second element of type should be one of the following.

nonparametric, which requests a nonparametric spline
parametric, which requests a parametric spline

If parametric is specified, a parameter sequence $\{t_i\}$ is formed as follows:

and

$t_i=t_{i-1} + \sqrt{ (x_i - x_{i-1})^2 + (y_i - y_{i-1})^2 }$

Splines are then fit to both the first and second columns of data. The resulting splined values are paired to form the output. Changing the relative scaling of the first two columns of data changes the output because the sequence $\{t_i\}$ assumes Euclidean distance.

Note that if the points are not arranged in strictly ascending order by the first columns of data, then a parametric method must be used. An error message results if the nonparametric spline is requested.

slope

is an optional

matrix of endpoint slopes given as angles in degrees. If a parametric spline is used, the angle values are used modulo 360. If a nonparametric spline is used, the tangent of the angles is used to set the slopes (that is, the effective angles range from -90 to 90 degrees).

Refer to Stoer and Bulirsch (1980), Reinsch (1967), and Pizer (1975) for descriptions of the methods used to fit the spline. For simplicity, the following explanation assumes that the data matrix does not contain a weighting column.

Nonparametric splines can be used to fit data for which you believe there is a functional relationship between the X and Y variables. The unique values of X (stored in the first column of data) form a partition $\{a=x_1 \lt x_2 \lt ... \lt x_n=b \}$ of the interval . You can use a spline to interpolate the data (produce a curve that passes through each data point) provided that there is a single Y value for each X value. The spline is created by constructing cubic polynomials on each subinterval $[x_i, x_{i+1}]$ so that the value of the cubic polynomials and their first two derivatives coincide at each .

An interpolating spline is not uniquely determined by the set of Y values. To achieve a unique interpolant, , you must specify two constraints on the endpoints of the interval . You can achieve uniqueness by specifying one of the following conditions:

The second derivative at both endpoints is zero. This is the default condition, but can be explicitly set by using type='zero'.
Periodic conditions. If your data are periodic so that 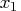can be identified with , and if , then the interpolating spline already satisfies . Setting type='periodic' further requires that and .
Fixed slopes at endpoints. Setting slope= requires that and .

The following code gives three examples of computing an interpolating spline for data. Note that the first and last Y values are the same, so you can ask for a periodic spline.

  
    data = { 0 5, 1 3, 2 5, 3 4, 4 6, 5 7, 6 6, 7 5 }; 
  
    /* Compute three spline interpolants of the data */ 
    /* (1) a cubic spline with type=zero (the default) */ 
    call spline(fitted,data); 
  
    /* (2) A periodic spline */ 
    call spline(periodicFitted,data) type='periodic'; 
  
    /* (3) A spline with specific slopes at endpoints */ 
    call spline(slopeFitted,data) slope={45 30};

You can also use a spline to smooth data. In general, a smoothing spline will not pass through any data pair exactly. A very small value of the smooth smoothing parameter will approximate an interpolating polynomial for data in which each unique X value is assigned the mean of the Y values corresponding to that X value. As the smooth parameter gets very large, the spline will approximate a linear regression.

The following code computes two smoothing splines for the same data as in the previous example. The spline coefficients are passed to the SPLINEV function which evaluates the smoothing spline at the original X values. Note that the smoothing spline does not pass through the original Y values. Note also that the smoothing parameter for the periodic spline is smaller, so the periodic spline has more "wiggles" than the corresponding spline with the larger smoothing parameter.

  
    data = { 0 5, 1 3, 2 5, 3 4, 4 6, 5 7, 6 6, 7 5 }; 
  
    /* Compute spline smoothers of the data. */ 
    call splinec(fitted,coeff,endSlopes,data) smooth=1; 
  
    /* Evaluate the smoother at the original X positions */ 
    smoothFit = splinev(coeff, data[,1]); 
  
    /* Compute periodic spline smoother of the data. */ 
    call splinec(fitted,coeff,endSlopesP,data) 
                 smooth=0.1 type='periodic'; 
  
    /* Evaluate the smoother at the original X positions */ 
    smoothPeriodicFit = splinev(coeff, data[,1]); 
  
    /* Compare the two fits. Verify that the periodic 
       spline has identical slopes at the end points. */ 
    print smoothFit smoothPeriodicFit, endSlopesP;

  
                 SMOOTHFIT           SMOOTHPERIODICFIT 
  
                 0 4.4761214             0 4.7536432 
                 1  4.002489             1 3.5603915 
                 2 4.2424509             2 4.3820561 
                 3 4.8254655             3   4.47148 
                 4 5.7817386             4 5.8811872 
                 5 6.3661254             5 6.8331581 
                 6 6.0606327             6 6.1180839 
                 7 5.2449764             7 4.7536432 
  
                              ENDSLOPESP 
  
                         -58.37255 -58.37255

A parametric spline can be used to interpolate or smooth data for which there does not seem to be a functional relationship between the X and Y variables. A partition $\{t_i\}$ is formed as explained in the documentation for the type parameter. Splines are then used to fit the X and Y values independently.

The following program fits a parametric curve to data that is shaped like an "S." The variable fitted is returned as a numParam matrix that contains the ordered pairs corresponding to the parametric spline. These ordered pairs correspond to numParam evenly spaced points in the domain of the parameter .

The purpose of the SPLINEV function is to evaluate (or score) an interpolating or smoothing spline at an arbitrary set of points. The following program shows how to construct the parameters corresponding to the original data by using the formula specified in the documentation for the type argument. These parameters are used to construct the evenly spaced parameters corresponding to the data in the fitted matrix.

  
    data = {3 7, 2 7, 1 6, 1 5, 2 4, 3 3, 3 2, 2 1, 1 1}; 
  
    /* Compute parametric spline interpolant */ 
    numParam = 20; 
    call splinec(fitted,coeff,endSlopes,data) 
                 nout=numParam type={'zero' 'parametric'}; 
  
    /* Form the parameters mapped onto the data */ 
    /* Evaluating the splines at t would return data */ 
    t = j(nrow(data),1,0); /* first parameter is zero */ 
    do i = 2 to nrow(t); 
       t[i] = t[i-1] + sqrt( (data[i,1]-data[i-1,1])##2 + 
                             (data[i,2]-data[i-1,2])##2 ); 
    end; 
  
    /* construct numParam evenly-spaced parameters 
       between 0 and t[nrow(t)] */ 
    params = do(0, t[nrow(t)], t[nrow(t)]/(numParam-1))`; 
  
    /* evaluate the parametric spline at these points */ 
    xy = splinev(coeff, params); 
    print params fitted xy;

The output from this program is as follows:

  
  
  
    PARAMS       FITTED                     XY 
  
         0            3         7            3         7 
 0.6897753    2.3002449 7.0492667    2.3002449 7.0492667 
 1.3795506    1.6566257 6.8416091    1.6566257 6.8416091 
 2.0693259    1.1581077 6.3289203    1.1581077 6.3289203 
 2.7591012    0.9203935 5.6475064    0.9203935 5.6475064 
 3.4488765    1.0128845 4.9690782    1.0128845 4.9690782 
 4.1386518    1.4207621 4.4372889    1.4207621 4.4372889 
 4.8284271            2         4            2         4 
 5.5182024    2.5792379 3.5627111    2.5792379 3.5627111 
 6.2079777    2.9871155 3.0309218    2.9871155 3.0309218 
  6.897753    3.0796065 2.3524936    3.0796065 2.3524936 
 7.5875283    2.8418923 1.6710797    2.8418923 1.6710797 
 8.2773036    2.3433743 1.1583909    2.3433743 1.1583909 
 8.9670789    1.6997551 0.9507333    1.6997551 0.9507333 
 9.6568542            1         1            1         1

Attempting to evaluate a spline outside of its domain of definition will result in a missing value. For example, the following code defines a spline on the interval . Attempting to evaluate the spline at points outside of this interval (-1 or 20) results in missing values.

  
    data = { 0 5, 1 3, 2 5, 3 4, 4 6, 5 7, 6 6, 7 5 }; 
    call splinec(fitted,coeff,endSlopes,data) slope={45 45}; 
    v =  splinev(coeff,{-1 1 2 3 3.5 4 20}); 
    print v; 
  
                                V 
  
                            -1         . 
                             1         3 
                             2         5 
                             3         4 
                           3.5 4.7073171 
                             4         6 
                            20         .

One use of splines is to estimate the integral of a function that is known only by its value at a discrete set of points. Many people are familiar with elementary methods of numerical integration such as the Left-Hand Rule, the Trapezoid Rule, and Simpson's Rule. In the Left-Hand Rule, the integral of discrete data is estimated by the exact integral of a piecewise constant function between the data. In the Trapezoid Rule, the integral is estimated by the exact integral of a piecewise linear function connecting the data. In Simpson's Rule, the integral is estimated as the exact integral of a piecewise quadratic function between the data points.

Since a cubic spline is a sequence of cubic polynomials, it is possible to compute the exact integral of the cubic spline and use this as an estimate for the integral of the discrete data. The next example takes a function defined by discrete data and finds the integral and the first moment of the function.

The implementation of the integrand function (fcheck) uses a useful trick to evaluate a spline at a single point. Note that if you pass in a scalar argument to the SPLINEV function, you get back a vector that represents the evaluation of the spline along evenly spaced points. To get around this, the function evaluates the spline at the vector x // x and then takes the entry in the first row, second column. This number is the value of the spline evaluated at . Here is the code:

  
    x = { 0, 2, 5, 7, 8, 10 }; 
    y = x + 0.1*sin(x); 
    a = x || y; 
    call splinec(fit,coeff,endSlopes,a); 
  
    start fcheck(x) global(coeff,pow); 
       /* The first column of v contains the points of evaluation 
          while the second column contains the evaluation. */ 
       v = x##pow # splinev(coeff,x //x)[1,2]; 
       return(v); 
    finish; 
  
    /* use QUAD to integrate */ 
    start moment(po) global(coeff,pow); 
       pow = po; 
       call quad(z,'fcheck',coeff[,1]) eps = 1.e-10; 
       v1  = sum(z); 
       return(v1); 
    finish; 
  
    mass  = moment(0);   /* to compute the mass */ 
    mass  = mass // 
           (moment(1)/mass) // /* to compute the mean */ 
           (moment(2)/mass) ;  /* to compute the meansquare */ 
    print mass; 
  
    /* Check the computation by using Gauss-Legendre integration: this 
       is good for moments up to maxng. */ 
  
    gauss = { 
        -9.3246951420315205e-01 
        -6.6120938646626448e-01 
        -2.3861918608319743e-01 
         2.3861918608319713e-01 
         6.6120938646626459e-01 
         9.3246951420315183e-01, 
         1.713244923791701e-01 
         3.607615730481388e-01 
         4.679139345726905e-01 
         4.679139345726904e-01 
         3.607615730481389e-01 
         1.713244923791707e-01  }; 
    ngauss = ncol(gauss); 
    maxng  =  2*ngauss-4; 
  
    start moment1(pow) global(coeff,gauss,ngauss,maxng); 
       if pow < maxng  then do; 
          nrow    = nrow(coeff); 
          ncol    = ncol(coeff); 
          left    = coeff[1:nrow-1,1]; 
          right   = coeff[2:nrow,1]; 
          mid     = 0.5*(left+right); 
          interv  = 0.5*(right - left); 
          /* scale the weights on each interval */ 
          wgts    = shape(interv*gauss[2,],1); 
          /* scale the points on each interval */ 
          pts     = shape(interv*gauss[1,] + mid * repeat(1,1,ngauss),1) ; 
          /* evaluate the function */ 
          eval    = splinev(coeff,pts)[,2]`; 
          mat     = sum (wgts#pts##pow#eval); 
       end; 
       return(mat); 
    finish; 
  
    mass  = moment1(0);       /* to compute the mass */ 
    mass  = mass // (moment1(1)/mass) //  (moment1(2)/mass) ; 
    print mass; /* should agree with earlier result */

The program prints the following results:

Top of Page