Language Reference: RATIO Function :: SAS/IML(R) 9.2 User's Guide

Language Reference

RATIO Function

divides matrix polynomials

returns a matrix containing the terms of $\phi (b)^{-1} \theta (b)$ considered as a matrix of rational functions in that have been expanded as power series

RATIO( ar, ma, terms<, dim>)

The inputs to the RATIO function are as follows:

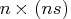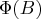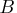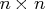ar: is an matrix representing a matrix polynomial generating function, $\phi (b)$ , in the variable . The first submatrix represents the constant term and must be nonsingular, the second 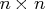submatrix represents the first-order coefficients, and so on.
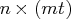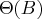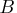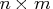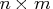ma: is an matrix representing a matrix polynomial generating function, $\theta (b)$ , in the variable . The first submatrix represents the constant term, the second submatrix represents the first-order term, and so on.
terms: is a scalar containing the number of terms to be computed, denoted by 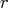in the following discussion. This value must be positive.
dim: is a scalar containing the value of 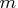, a dimension of the matrix ma. The default value is 1.

The RATIO function multiplies a matrix of polynomials by the inverse of another matrix of polynomials. It is useful for expressing univariate and multivariate ARMA models in pure moving-average or pure autoregressive forms.

The value returned is an

matrix containing the terms of $\phi (b)^{-1} \theta (b)$ considered as a matrix of rational functions in

that have been expanded as power series.

Note: The RATIO function can be used to consolidate the matrix operators employed in a multivariate time series model of the form

$\phi (b) y_t = \theta (b) \epsilon_t$

where $\phi (b)$ and $\theta (b)$ are matrix polynomial operators whose first matrix coefficients are identity matrices. The RATIO function can be used to compute a truncated form of $\psi (b) = \phi (b)^{-1} \theta (b)$ for the equivalent infinite-order model

$y_t = \psi (b) \epsilon_t$

The RATIO function can also be employed for simple scalar polynomial division, giving a truncated form of $\theta (x)/\phi (x)$ for two scalar polynomials $\theta (x)$ and $\phi (x)$ .

The cumulative sum of the elements of a column vector can be obtained by using the following statement:

  
     ratio({ 1 -1} ,x,ncol(x));

Consider the following example for multivariate ARMA(1,1):

  
       ar={1 0 -.5  2, 
           0 1   3 -.8}; 
       ma={1 0 .9  .7, 
           0 1   2 -.4}; 
       psi=ratio(ar,ma,4,2);

The matrix produced is as follows:

  
            PSI 
              1    0   1.4  -1.3   2.7  -1.45  11.35 
    :    -9.165 
  
              0    1    -1   0.4   -5   4.22  -12.1 
    :     7.726

Top of Page