Language Reference: PRODUCT Function :: SAS/IML(R) 9.2 User's Guide

Language Reference

PRODUCT Function

multiplies matrices of polynomials

PRODUCT( 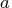, 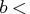$b\lt$ , dim>)

The inputs to the PRODUCT function are as follows:

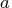
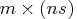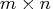: is an numeric matrix. The first submatrix contains the constant terms of the polynomials, the second 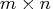submatrix contains the first-order terms, and so on.
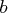
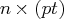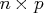: is an matrix. The first submatrix contains the constant terms of the polynomials, the second 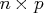submatrix contains the first-order terms, and so on.
dim: is a 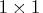matrix, with value 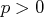$p\gt$ . The value of this matrix is used to set the dimension 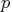of the matrix 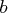. If omitted, the value of 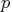is set to 1.

The PRODUCT function multiplies matrices of polynomials. The value returned is the

matrix of the polynomial products. The first

submatrix contains the constant terms, the second

submatrix contains the first-order terms, and so on.

Note: The PRODUCT function can be used to multiply the matrix operators employed in a multivariate time series model of the form

$\phi_1(b) \phi_2(b) y_t = \theta_1(b) \theta_2(b) \epsilon_t$

where $\phi_1(b)$ , $\phi_2(b)$ , $\theta_1(b)$ , and $\theta_2(b)$ are matrix polynomial operators whose first matrix coefficients are identity matrices. Often $\phi_2(b)$ and $\theta_2(b)$ represent seasonal components that are isolated in the modeling process but multiplied with the other operators when forming predictors or estimating parameters. The RATIO function is often employed in a time series context as well.

For example, the following statement produces the matrix , as shown:

  
    r=product({1 2 3 4, 
               5 6 7 8}, 
              {1 2 3, 
               4 5 6}, 1);

  
                 R             2 rows      4 cols    (numeric) 
  
                            9        31        41        33 
                           29        79       105        69

Top of Page