Genetic Algorithms: Using Crossover and Mutation Operators

Genetic Algorithms

Using Crossover and Mutation Operators

IML enables you to employ user modules for crossover and mutation operators, or you may choose from the operators provided by IML. The IML operators are tied to the problem encoding options, and IML will check to make sure a specified operator is appropriate to the problem encoding. You can also turn off crossover, in which case the current population will pass on to the next generation subject only to mutation. Mutation can be turned off by setting the mutation probability to 0.

The IML-supplied genetic operators are described below, beginning with the crossover operators:

simple:

This operator is defined for fixed-length integer and real vector encoding. To apply this operator, a position k within a vector of length

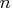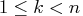is chosen at random, such that $1 \leq k \lt n$ . Then for parents p1 and p2 the offspring are

  
 c1= p1[1,1:k] || p2[1,k+1:n]; 
  
 c2= p2[1,1:k] || p1[1,k+1:n];

For real fixed-length vector encoding, you can specify an additional parameter,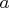

, where

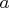is a scalar and 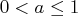$0 \lt a \leq 1$ . It modifies the offspring as follows:

  
 x2 = a * p2 + (1-a) * p1; 
 c1 = p1[1,1:k] || x2[1,k+1:n]; 
  
 x1 = a * p1 + (1-a) * p2 
 c2 = p2[1,1:k] || x1[1,k+1:n];

Note that for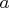

= 1, which is the default value, x2 and x1 are the same as p2 and p1. Small values of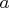

reduce the difference between the offspring and parents. For integer encoding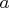

is always 1.

two-point:

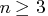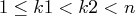This operator is defined for fixed-length integer and real vector encoding with length $n \geq 3$ . To apply this operator, two positions k1 and k2 within the vector are chosen at random, such that $1 \leq k1 \lt k2 \lt n$ . Element values between those positions are swapped between parents. For parents p1 and p2 the offspring are

  
 c1 = p1[1,1:k1] || p2[1,k1+1:k2] || p1[1,k2+1:n]; 
  
 c2 = p2[1,1:k1] || p1[1,k1+1:k2] || p2[1,k2+1:n];

For real vector encoding you can specify an additional parameter,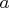

, where 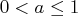$0 \lt a \leq 1$ . It modifies the offspring as follows:

  
 x2 = a * p2 + (1-a) * p1; 
 c1 = p1[1,1:k1] || x2[1,k1+1:k2] || p1[1,k2+1:n]; 
  
 x1 = a * p1 + (1-a) * p2; 
 c2 = p2[1,1:k1] || x1[1,k1+1:k2] || p2[1,k2+1:n];

Note that for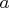

= 1, which is the default value, x2 and x1 are the same as p2 and p1. Small values of a reduce the difference between the offspring and parents. For integer encoding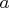

is always 1.

arithmetic:

This operator is defined for real and integer fixed-length vector encoding. This operator computes offspring of parents p1 and p2 as

  
 c1 = a * p1 + (1-a) * p2; 
  
 c2 = a * p2 + (1-a) * p1;

where a is a random number between 0 and 1. For integer encoding, each component is rounded off to the nearest integer. It has the advantage that it will always produce feasible offspring for a convex solution space. A disadvantage of this operator is that it will tend to produce offspring toward the interior of the search region, so that it may be less effective if the optimum lies on or near the search region boundary.

heuristic:

This operator is defined for real fixed-length vector encoding. It computes the first offspring from the two parents p1 and p2 as

  
        c1 = a * (p2 - p1) + p2;

where p2 is the parent with the better objective value, and a is a random number between 0 and 1. The second offspring is computed as in the arithmetic operator:

  
        c2 = (1 - a) * p1 + a * p2;

This operator is unusual in that it uses the objective value. It has the advantage of directing the search in a promising direction, and automatically fine-tuning the search in an area where solutions are clustered. If the solution space has upper and lower bound constraints the offspring will be checked against the bounds, and any component outside its bound will be set equal to that bound. The heuristic operator will perform best when the objective function is smooth, and may not work well if the objective function or its first derivative is discontinuous.

pmatch:

The partial match operator is defined for sequence encoding. It produces offspring by transferring a subsequence from one parent, and filling the remaining positions in a way consistent with the position and ordering in the other parent. Start with two parents and randomly chosen cutpoints as indicated:

  
        p1 = {1 2|3 4 5 6|7 8 9}; 
        p2 = {8 7|9 3 4 1|2 5 6};

The first step is to cross the selected segments ( . indicates positions yet to be determined):

  
        c1 = {. . 9 3 4 1 . . .}; 
        c2 = {. . 3 4 5 6 . . .};

Next, define a mapping according to the two selected segments:

  
        9-3, 3-4, 4-5, 1-6

Next, fill in the positions where there is no conflict from the corresponding parent:

  
        c1 = {. 2 9 3 4 1 7 8 .}; 
        c2 = {8 7 3 4 5 6 2 . .};

Last, fill in the remaining positions from the subsequence mapping. In this case, for the first chil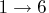d

and

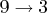, and for the second child

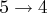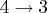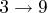and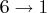

  
        c1 = {6 2 9 3 4 1 7 8 5}; 
        c2 = {8 7 3 4 5 6 2 9 1};

This operator will tend to maintain similarity of both the absolute position and relative ordering of the sequence elements, and is useful for a wide range of sequencing problems.

order:

This operator is defined for sequence encoding. It produces offspring by transferring a subsequence of random length and position from one parent, and filling the remaining positions according to the order from the other parent. For parents p1 and p2, first choose a subsequence:

  
        p1 = {1 2|3 4 5 6|7 8 9}; 
        p2 = {8 7|9 3 4 1|2 5 6}; 
  
        c1 = {. . 3 4 5 6 . . .}; 
        c2 = {. . 9 3 4 1 . . .};

Starting at the second cutpoint, the elements of p2 in order are (cycling back to the beginning)

  
        2 5 6 8 7 9 3 4 1

After removing 3, 4, 5 and 6, which have already been placed in c1, we have

  
        2 8 7 9 1

Placing these back in order starting at the second cutpoint yields

  
        c1 = {9 1 3 4 5 6 2 8 7};

Applying this logic to c2 yields

  
        c2 = {5 6 9 3 4 1 7 8 2};

This operator maintains the similarity of the relative order, or adjacency, of the sequence elements of the parents. It is especially effective for circular path-oriented optimizations, such as the traveling salesman problem.

cycle:

This operator is defined for sequence encoding. It produces offspring such that the position of each element value in the offspring comes from one of the parents. For example, for parents p1 and p2,

  
           p1 = {1 2 3 4 5 6 7 8 9}; 
           p2 = {8 7 9 3 4 1 2 5 6};

For the first child, pick the first element from the first parent:

  
           c1 = {1 . . . . . . . .};

To maintain the condition that the position of each element value must come from one of the parents, the position of the '8' value must come from p1, because the '8' position in p2 is already taken by the '1' in c1:

  
           c1 = {1 . . . . . . 8 .};

Now the position of '5' must come from p1, and so on until the process returns to the first position:

  
           c1 = {1 . 3 4 5 6 . 8 9};

At this point, choose the remaining element positions from p2:

  
           c1 = {1 7 3 4 5 6 2 8 9};

For the second child, starting with the first element from the second parent, similar logic produces

  
           c2 = {8 2 9 3 4 1 7 5 6};

This operator is most useful when the absolute position of the elements is of most importance to the objective value.

The mutation operators supported by IML are as follows:

uniform:

This operator is defined for fixed-length real or integer encoding with specified upper and lower bounds. To apply this operator, a position k is randomly chosen within the solution vector v, and v[k] is modified to a random value between the upper and lower bounds for element k. This operator may prove especially useful in early stages of the optimization, since it will tend to distribute solutions widely across the search space, and avoid premature convergence to a local optimum. However, in later stages of an optimization with real vector encoding, when the search needs to be fine-tuned to home in on an optimum, the uniform operator may hinder the optimization.

delta:

This operator is defined for integer and real fixed-length vector encoding. It first chooses an element of the solution at random, and then perturbs that element by a fixed amount, set by a delta input parameter. delta has the same dimension as the solution vectors. To apply the mutation, a randomly chosen element k of the solution vector v is modified such that

  
 v[k] = v[k] + delta[k]; /* with probability 0.5 */ 
         or 
 v[k] = v[k] - delta[k];

If upper and lower bounds are specified for the problem, then v[k] is adjusted as necessary to fit within the bounds. This operator gives you the ability to control the scope of the search with the delta vector. One possible strategy is to start with a larger delta value, and then reduce it as the search progresses and begins to converge to an optimum. This operator is also useful if the optimum is known to be on or near a boundary, in which case delta can be set large enough to always perturb the solution element to a boundary.

swap:

This operator is defined for sequence problem encoding. It picks two random locations in the solution vector, and swaps their value. You can also specify that multiple swaps be made for each mutation.

invert:

This operator is defined for sequence encoding. It picks two locations at random, and then reverses the order of elements between them. This operator is most often applied to the traveling salesman problem.

The IML-supplied crossover and mutation operators that are allowed for each problem encoding are summarized in the following table.

Table 17.1: Valid Genetic Operators for Each Encoding

Encoding	Crossover	Mutation
general	user module	user module
fixed-length real vector	user module	user module
	simple	uniform
	two-point	delta
	arithmetic
	heuristic
fixed-length integer vector	user module	user module
	simple	uniform
	two-point	delta
	arithmetic
fixed-length integer sequence	user module	user module
	pmatch	swap
	order	invert
	cycle

A user module specified as a crossover operator must be a subroutine with four parameters. The module should compute and return two new offspring solutions in the first two parameters, based on the two parent solutions, which will be passed into the module in the last two parameters. The module should not modify the parent solutions passed into it. A global clause can be used to pass in any additional information that the module might use.

A user module specified as a mutation operator must be a subroutine with exactly one parameter. When the module is called, the parameter will contain the solution that is to be mutated. The module will be expected to update the parameter with the new mutated value for the solution. As with crossover, a global clause can be used to pass in any additional information that the module might use.

Top of Page