Model Overdispersion
Overdispersion is a phenomenon that occurs occasionally with binomial and Poisson data. For Poisson data, it occurs when the variance of
the response 
exceeds the Poisson variance. (Recall that the Poisson variance equals the response mean: 
.) To account for the overdispersion that might occur in the Ship data, you can specify a method for estimating the overdispersion.
To estimate overdispersion:
-
Select → → from the main menu.
Each tab of the dialog box initializes with the values from the previous analysis of these data.
-
Click the Method tab.
-
Select for the field (shown in Figure 24.21).
-
Click .
Figure 24.21: Modeling Overdispersion
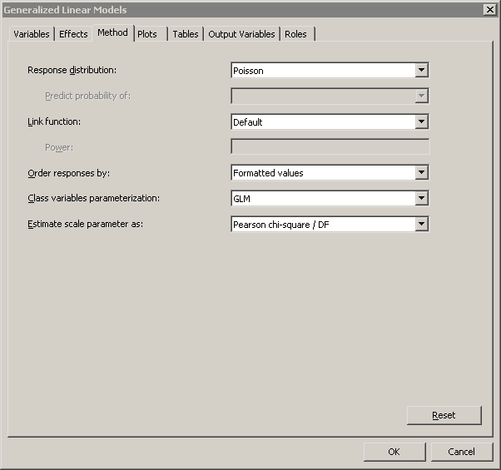
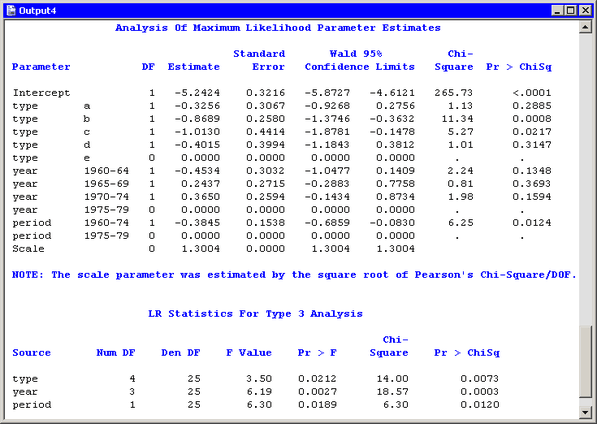
Figure 24.22 shows the output for the analysis.
A note states that “the scale parameter was estimated by the square root of Pearson’s Chi-Square/DOF.” The scale value reported in the “Analysis Of Maximum Likelihood Parameter Estimates” table is greater than 1, which suggests that overdispersion exists in the model.
Note that the parameter estimates are unchanged by the dispersion estimate. However, the estimate does affect the covariance matrix, standard errors, and log likelihoods used in likelihood ratio tests. A comparison of Figure 24.20 with Figure 24.22 shows multiple differences in the output statistics.
Although the estimate of the dispersion parameter is often used to indicate overdispersion or underdispersion, this estimate might also indicate other problems, such as an incorrectly specified model or outliers in the data. See the subsection “Generalized Linear Models Theory” in the “Details” section of the documentation for the GENMOD procedure for a discussion of the dispersion parameter and overdispersion.
Figure 24.22: Estimating the Overdispersion Parameter
