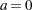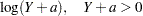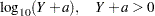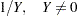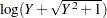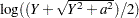Previous Page | Next Page

Variance Stabilizing Transformations

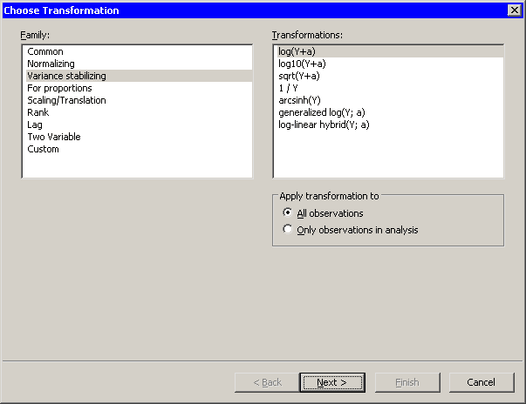
Figure 32.13 shows the transformations that are available when you select Variance stabilizing from the Family list. Variance stabilizing transformations are often used to transform a variable whose variance depends on the value of the variable. For example, the variability of a variable 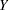$\text{[math]}$ might increase as 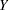$\text{[math]}$ increases. Equations for these transformations are given in Table 32.3.

Figure 32.13 Variance Stabilizing Transformations

Table 32.3 Description of Variance Stabilizing Transformations
Transformation	Parameter	New Variable	Equation
	Default	Name of
log(Y+a)	$\text{[math]}$	Log_Y	$\text{[math]}$
log10(Y+a)	$\text{[math]}$	Log10_Y	$\text{[math]}$
sqrt(Y+a)	$\text{[math]}$	Sqrt_Y	$\text{[math]}$
1 / Y		Inv_Y	$\text{[math]}$
arcsinh(Y)		Arcsinh_Y	$\text{[math]}$
generalized log(Y;a)	$\text{[math]}$	GLog_Y	$\text{[math]}$
log-linear hybrid(Y;a)	$\text{[math]}$	LogLin_Y	See text.

The log-linear hybrid transformation is defined for $\text{[math]}$ as follows:

$\text{[math]}$

The function is linear for 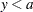$\text{[math]}$ , logarithmic for 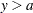$\text{[math]}$ , and continuously differentiable.

The generalized log and the log-linear hybrid transformations were introduced in the context of gene-expression microarray data by Rocke and Durbin (2003).