Example: Fit a Polynomial Curve to Data

In this example, you create a polynomial regression analysis of wind_kts as a function of min_pressure in the Hurricanes data set. The wind_kts variable is the wind speed in knots; the min_pressure variable is the minimum central pressure for each observation.

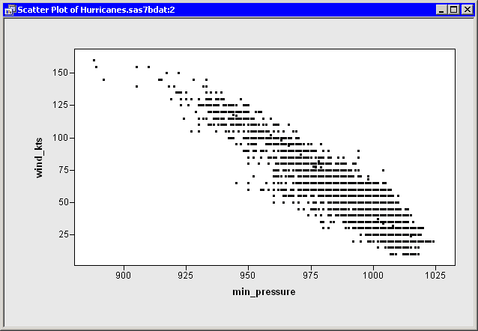
A scatter plot of these variables indicates that the relationship between these variables is approximately linear, as shown in Figure 20.1, so this example fits a line to the data.

Figure 20.1 Linearly Related Variables

To create a polynomial regression analysis:

1. Open the Hurricanes data set.

2. Select Analysis Data Smoothing Polynomial Regression from the main menu, as shown in Figure 20.2.

   Figure 20.2 Selecting Variables

   
   
   

   The Polynomial Regression dialog box appears. (See Figure 20.3.)

3. Select the variable wind_kts, and click Set Y.

4. Select the variable min_pressure, and click Set X.

   Figure 20.3 The Variables Tab

   
   
   

5. Click the Plots tab.

   The Plots tab becomes active. This tab controls which graphs are produced by the analysis, and the options for each graph (for example, whether to display confidence limits).

   By default, the analysis creates a scatter plot of the observed X and Y variables, with a smoother added. You can decide whether or not to plot confidence limits.

6. Clear Confidence limits for means.

7. Select Residual normal QQ.

8. Click OK.

   Figure 20.4 The Plots Tab

   
   
   

   Several plots appear, along with output from the REG procedure. (See Figure 20.5.) A scatter plot shows the bivariate data and the requested linear smoother. The analysis also creates a normal Q-Q plot of the residuals. The Q-Q plot indicates that quite a few observations have wind speeds that are substantially lower than would be expected by assuming a linear model with normally distributed errors. In Figure 20.5 these observations are selected, and the corresponding markers in the scatter plot are highlighted.

   Figure 20.5 Results from the Polynomial Regression Analysis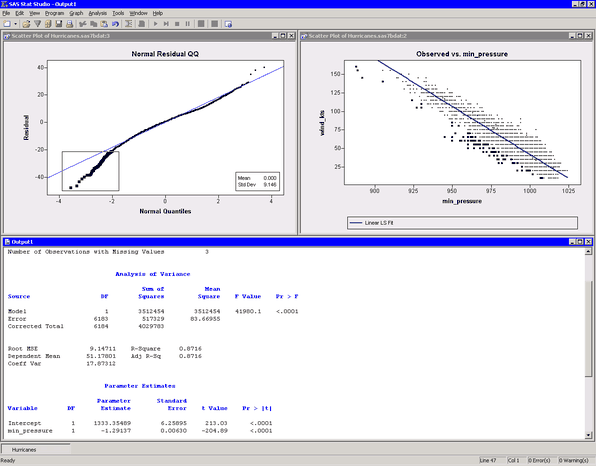

   
   
   

   Output from the REG procedure appears in the output document. The output informs you that min_pressure has three missing values; those observations are not included in the analysis. The parameter estimates table indicates that when the central atmospheric pressure of a cyclone decreases by 1 hPa, you can expect the wind speed to increase by about 1.3 knots.