Model Fitting: Generalized Linear Models: Revising the Model

Model Fitting: Generalized Linear Models

Revising the Model

In this section you remove the interaction effect from the previous model and refit the data.

Select Analysis $\blacktriangleright\,$ Model Fitting $\blacktriangleright\,$ Generalized Linear Models to redisplay the dialog box for this analysis.

Note: The items on the Analysis menu are not available if the output window is active. If the menu is not enabled, you should activate a graphical or tabular view of the data before clicking on the Analysis menu.

Click the Effects tab.

Select drug * disease from the Effects in Model list.

Click Remove.

The interaction term is removed from the list of effects, as shown in Figure 24.11.

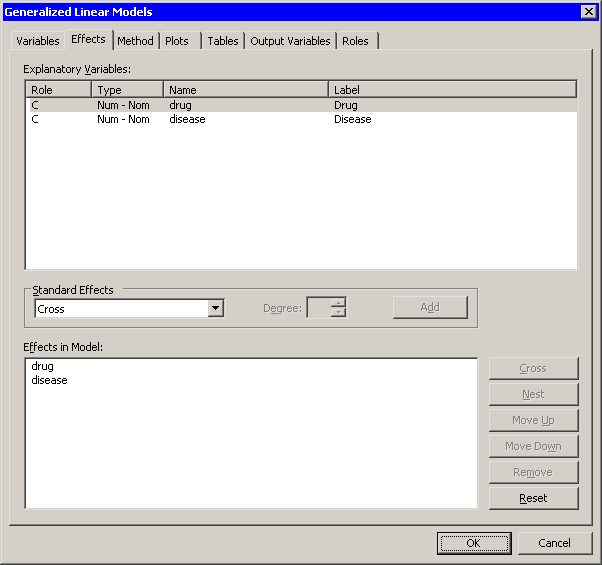Figure 24.11: Revising the Model

Click OK.

Move the workspace windows so that they are arranged as in Figure 24.12. The "LR Statistics For Type 3 Analysis" table indicates that both main effects are significant.

The "Analysis Of Maximum Likelihood Parameter Estimates" table displays parameter estimates for the model. You can use these values to determine the predicted mean response for each experimental group. The interpretation of the parameter estimates depends on the parameterization used to encode the classification variables in the model design matrix. This example used the GLM coding (see Figure 24.8). For this parameterization, the predicted response for a subject is obtained by adding the estimate for the intercept to the parameter estimates for the groups to which the subject belongs. For example, the predicted change in blood pressure in a subject with drug=1 and disease=2 is $8.9861 + 13.4444 + 5.2917 \approx 27.7.$

For a given level, the parameter estimate represents the difference between that level and the last level. For example, the estimate of the difference between the parameters for drug 1 and drug 4 is 13.4444, and this estimate is significantly different from zero (as indicated by the -value in the "Pr > ChiSq" column). In contrast, the difference in the coefficients between drug 3 and drug 4 is - 4.1667, but this estimate is not significantly different from zero. Similarly, the estimate of the difference between disease 2 and disease 3 is (marginally) not significant.

The parameter estimates table also estimates the scale parameter. For a normally distributed response, the scale parameter is the standard deviation of the response. See the documentation for the GENMOD procedure in the SAS/STAT User's Guide for additional details.

There are three plots in Figure 24.12. The plot of observed values versus predicted values (upper right in Figure 24.12) shows how well the model fits the data. Since this model assumes a normally distributed response with an identity link, the plot of chi-square residuals versus predicted values (lower right in Figure 24.12) is just an ordinary residual plot (see the "Residuals" section of the documentation for the GENMOD procedure). The observations fall along vertical lines because all observations with the ith drug and the jth disease have the same predicted value.

The scatter plot of Cook's (upper left in Figure 24.12) indicates which observations have a large influence on the parameter estimates. Influential observations (that is, those with relatively large values of Cook's ) are selected in the figure. The selected observations are highlighted in the other plots. Each observation corresponds to a large negative residual, indicating that the observed change in blood pressure for these subjects was substantially less than the model predicts.

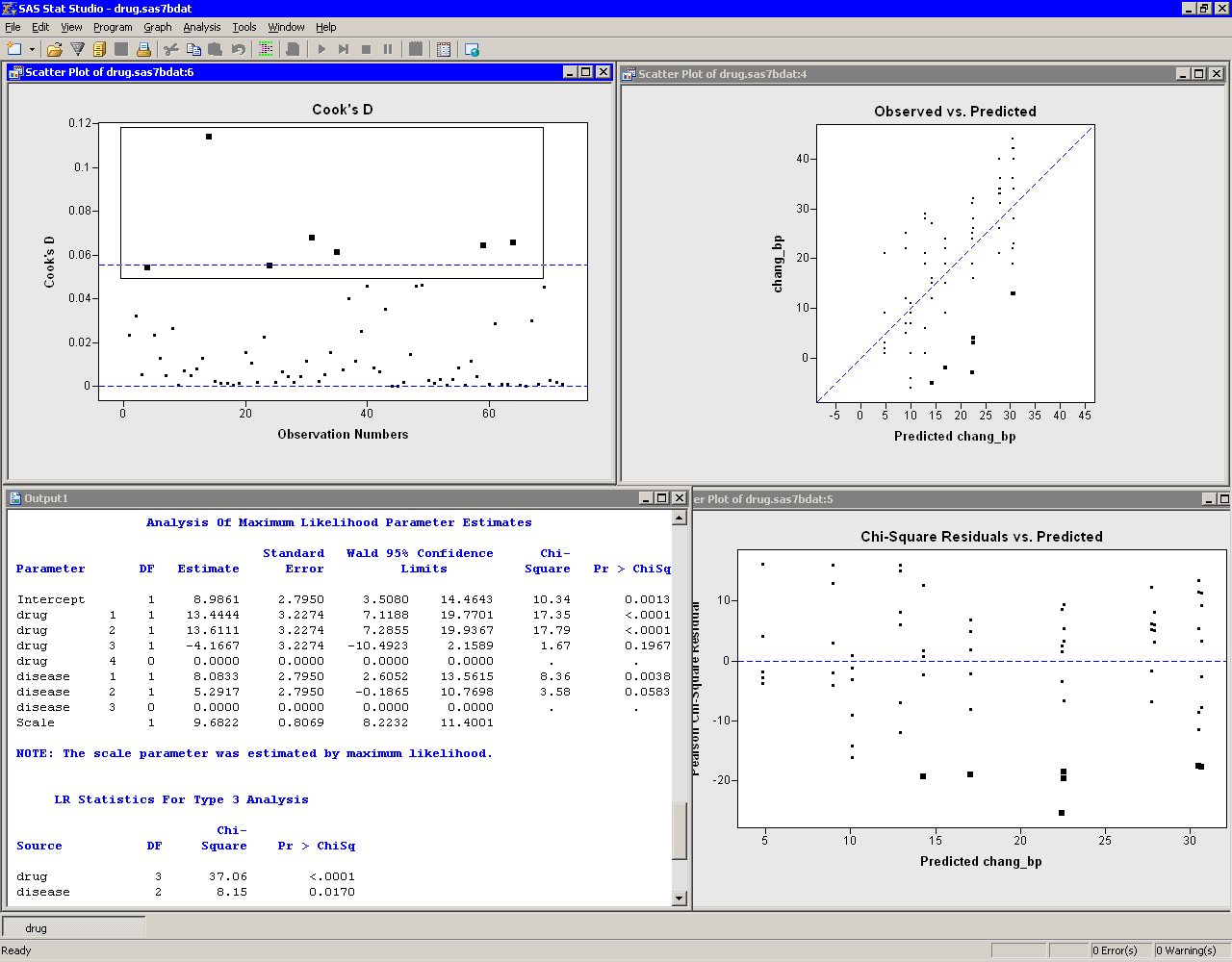Figure 24.12: A Revised Generalized Linear Models Analysis

Top of Page