| The ALLELE Procedure |
Linkage Disequilibrium (LD)
The set of genetic material an individual receives from each parent contains an allele at every locus, and statements can be made about these allelic combinations, or haplotypes. The probability  (called the gametic or haplotype frequency) that an individual receives the haplotype
(called the gametic or haplotype frequency) that an individual receives the haplotype  for marker loci M and N can be compared to the product of the probabilities that each allele is received. The difference is the linkage, or gametic, disequilibrium (LD) coefficient
for marker loci M and N can be compared to the product of the probabilities that each allele is received. The difference is the linkage, or gametic, disequilibrium (LD) coefficient  for those two alleles:
for those two alleles:  . There is a general expectation that the amount of linkage disequilibrium is inversely related to the distance between the two loci, but there are many other factors that can affect disequilibrium. There can even be disequilibrium between alleles at loci that are located on different chromosomes. Note that these tests and measures are calculated only for pairs of markers at most
. There is a general expectation that the amount of linkage disequilibrium is inversely related to the distance between the two loci, but there are many other factors that can affect disequilibrium. There can even be disequilibrium between alleles at loci that are located on different chromosomes. Note that these tests and measures are calculated only for pairs of markers at most  markers (or the unit used in the LOCATION variable of the NDATA= data set) apart, where
markers (or the unit used in the LOCATION variable of the NDATA= data set) apart, where  is the value specified in the MAXDIST= option of the PROC ALLELE statement (or 50 by default) when the WITH statement is omitted; otherwise, all pairs of markers containing one marker from the VAR statement and one from the WITH statement are examined.
is the value specified in the MAXDIST= option of the PROC ALLELE statement (or 50 by default) when the WITH statement is omitted; otherwise, all pairs of markers containing one marker from the VAR statement and one from the WITH statement are examined.
Table 3.1 displays how the HAPLO= option of the PROC ALLELE statement interacts with the linkage disequilibrium calculations. These calculations are discussed in more detail in the following two sections.
HAPLO= |
LD Test |
Estimate of |
|
|---|---|---|---|
Option |
Statistic |
LD Exact Test |
Haplotype Freq |
|
|
|
|
|
|||
EST |
|
Not performed |
Estimated freq, |
|
|
|
|
|
|||
|
|
|
|
|
Tests
When haplotypes are known, the HAPLO=GIVEN option should be included in the PROC ALLELE statement so that the linkage disequilibrium can be computed directly by substituting the observed frequencies  ,
,  , and
, and  into the equation in the preceding section for
into the equation in the preceding section for  . This creates the MLE,
. This creates the MLE,  , of the LD coefficient between a pair of alleles at different markers. PROC ALLELE calculates an overall chi-square statistic to test that all of the
, of the LD coefficient between a pair of alleles at different markers. PROC ALLELE calculates an overall chi-square statistic to test that all of the  ’s between two markers are zero as follows:
’s between two markers are zero as follows:
 |
which has  degrees of freedom for markers with
degrees of freedom for markers with  and
and  alleles, respectively.
alleles, respectively.
There is also a Monte Carlo estimate of the exact test available when haplotypes are known. An estimate of the exact  -value for testing the hypothesis in the preceding paragraph can be calculated by conditioning on the allele counts as with the permutation version of the exact test for HWE. The conditional probability of the haplotype counts is then
-value for testing the hypothesis in the preceding paragraph can be calculated by conditioning on the allele counts as with the permutation version of the exact test for HWE. The conditional probability of the haplotype counts is then
 |
and the significance level is obtained again by permuting the alleles at one locus to form 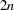 new two-locus haplotypes. You can indicate the number of permutations that are used in the PERMS= option of the PROC ALLELE statement and the random seed used to randomly permute the data in the SEED= option of the PROC ALLELE statement.
new two-locus haplotypes. You can indicate the number of permutations that are used in the PERMS= option of the PROC ALLELE statement and the random seed used to randomly permute the data in the SEED= option of the PROC ALLELE statement.
When it is requested that haplotype frequencies be estimated with the HAPLO=EST option,  is estimated using
is estimated using  , where
, where  is the MLE of
is the MLE of  assuming HWE. The estimate
assuming HWE. The estimate  is calculated according to the method described by Weir and Cockerham (1979). Again, a chi-square test statistic can be calculated to test that all of the
is calculated according to the method described by Weir and Cockerham (1979). Again, a chi-square test statistic can be calculated to test that all of the  ’s between a pair of markers are zero as
’s between a pair of markers are zero as
 |
which has  degrees of freedom for markers with
degrees of freedom for markers with  and
and  alleles, respectively. No exact test is available when haplotype frequencies are estimated.
alleles, respectively. No exact test is available when haplotype frequencies are estimated.
The HAPLO=NONE and HAPLO=NONEHWD options indicate that haplotypes are unknown and  should not be used in the tests for LD between pairs of markers. Instead of using the estimated haplotype frequencies which assumes HWE, a test can be formed using the composite linkage disequilibrium (CLD) coefficient
should not be used in the tests for LD between pairs of markers. Instead of using the estimated haplotype frequencies which assumes HWE, a test can be formed using the composite linkage disequilibrium (CLD) coefficient  that does not require this assumption and uses only allele and two-locus genotype frequencies. The MLE
that does not require this assumption and uses only allele and two-locus genotype frequencies. The MLE  of
of  can be calculated as described by Weir (1979), and a chi-square statistic that tests all
can be calculated as described by Weir (1979), and a chi-square statistic that tests all  ’s between a pair of markers are zero can be formed as follows:
’s between a pair of markers are zero can be formed as follows:
 |
which has  degrees of freedom for markers with
degrees of freedom for markers with  and
and  alleles, respectively. This statistic is used when HAPLO=NONE is specified. When each marker in the pair being analyzed is biallelic, a correction in this test statistic for departures from HWE can be requested with the HAPLO=NONEHWD option. The 1 df chi-square statistic is then represented as
alleles, respectively. This statistic is used when HAPLO=NONE is specified. When each marker in the pair being analyzed is biallelic, a correction in this test statistic for departures from HWE can be requested with the HAPLO=NONEHWD option. The 1 df chi-square statistic is then represented as
 |
with  .
.
Permutation versions of exact tests for CLD are given by Zaykin, Zhivotovsky, and Weir (1995), either assuming HWE or accounting for departures from HWE. The conditional probability of the two-locus genotypes given the one-locus alleles assuming HWE is
 |
where  is the count of
is the count of  genotypes,
genotypes,  and
and  are the counts of
are the counts of  and
and  alleles, respectively, and
alleles, respectively, and  represents the number of loci that are heterozygous for genotype
represents the number of loci that are heterozygous for genotype  (0, 1, or 2). An estimate of the exact significance level is obtained by permuting the alleles at both of the loci and counting a permuted sample toward the
(0, 1, or 2). An estimate of the exact significance level is obtained by permuting the alleles at both of the loci and counting a permuted sample toward the  -value when its probability
-value when its probability  is not larger than for the observed sample.
is not larger than for the observed sample.
When departures from HWE are accounted for, the conditional probability of the two-locus genotypes given the one-locus genotypes is
 |
with  and
and 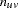 as the counts of
as the counts of  and
and  genotypes, respectively. An estimate of the exact significance level is obtained by permuting the genotypes at one of the loci and calculating the probability
genotypes, respectively. An estimate of the exact significance level is obtained by permuting the genotypes at one of the loci and calculating the probability  for each permuted sample. When HAPLO=NONEHWD is specified, the
for each permuted sample. When HAPLO=NONEHWD is specified, the  -value is reported as the proportion of samples that have a
-value is reported as the proportion of samples that have a  less than or equal to the one from the original sample.
Note:
less than or equal to the one from the original sample.
Note: can be used for multiallelic markers, while the formula for the chi-square statistic cannot. When HAPLO=NONEHWD, the chi-square statistic and asymptotic
can be used for multiallelic markers, while the formula for the chi-square statistic cannot. When HAPLO=NONEHWD, the chi-square statistic and asymptotic  -value that are reported for a marker with more than two alleles do not account for departures from HWE; however, the estimate of the exact
-value that are reported for a marker with more than two alleles do not account for departures from HWE; however, the estimate of the exact  -value does make this adjustment as expected.
-value does make this adjustment as expected.
Measures
PROC ALLELE offers several linkage disequilibrium measures to be calculated for each pair of alleles 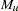 and
and  located at loci M and N, respectively. Devlin and Risch (1995) discuss the correlation coefficient
located at loci M and N, respectively. Devlin and Risch (1995) discuss the correlation coefficient  , the population attributable risk
, the population attributable risk  , Lewontin’s
, Lewontin’s 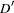 , the proportional difference
, the proportional difference  , and Yule’s
, and Yule’s  ; Morton et al. (2001) define
; Morton et al. (2001) define 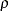 and its information
and its information  , which is calculated under the null hypothesis that
, which is calculated under the null hypothesis that  and also included in the "Linkage Disequilibrium Measures" table when the RHO option is specified. Since these measures are designed for biallelic markers, the measures are calculated for each allele at locus M with each allele at locus N, where all other alleles at each loci are combined to represent one allele. Thus for each allele
and also included in the "Linkage Disequilibrium Measures" table when the RHO option is specified. Since these measures are designed for biallelic markers, the measures are calculated for each allele at locus M with each allele at locus N, where all other alleles at each loci are combined to represent one allele. Thus for each allele 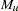 in turn,
in turn,  is used as the frequency of allele
is used as the frequency of allele 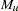 , and
, and  represents the frequency of "not
represents the frequency of "not 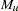 "; similarly for each
"; similarly for each  in turn,
in turn,  represents the frequency of allele
represents the frequency of allele  , and
, and  represents the frequency of "not
represents the frequency of "not  ." All measures have the same numerator,
." All measures have the same numerator,  , the LD coefficient, which can be directly estimated using the observed haplotype frequencies
, the LD coefficient, which can be directly estimated using the observed haplotype frequencies  when HAPLO=GIVEN, or estimated using the MLEs of the haplotype frequencies
when HAPLO=GIVEN, or estimated using the MLEs of the haplotype frequencies  assuming HWE when HAPLO=EST. The computations for the measures are as follows:
assuming HWE when HAPLO=EST. The computations for the measures are as follows:
 |
 |
 |
|||
 |
 |
 |
|||
 |
 |
 |
|||
 |
 |
 |
|||
 |
 |
 |
|||
 |
 |
 |
with estimates of measures calculated by replacing parameters with their appropriate estimates. Under the option HAPLO=NONE (the default) or HAPLO=NONEHWD, the numerator  can be replaced by the CLD coefficient
can be replaced by the CLD coefficient  , described in the preceding section, for measures
, described in the preceding section, for measures  and
and 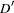 . The bounds for
. The bounds for  (
( ) given by Hamilton and Cole (2004) and Zaykin (2004) are used in place of the preceding formula for the denominator of
) given by Hamilton and Cole (2004) and Zaykin (2004) are used in place of the preceding formula for the denominator of 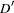 . The denominator of the correlation coefficient
. The denominator of the correlation coefficient  is adjusted for departures from HWE when HAPLO=NONEHWD in the same manner as the corresponding chi-square statistic, so that
is adjusted for departures from HWE when HAPLO=NONEHWD in the same manner as the corresponding chi-square statistic, so that  . The measures
. The measures  ,
,  ,
, 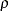 , and
, and  cannot be calculated for either of these two options. The information
cannot be calculated for either of these two options. The information  is estimated by
is estimated by  , where
, where  and
and  is the smaller allele frequency (
is the smaller allele frequency ( or
or  ) at the locus not used for
) at the locus not used for  .
.
Copyright © 2008 by SAS Institute Inc., Cary, NC, USA. All rights reserved.










