The PDLREG Procedure

Polynomial Distributed Lag Estimation

The simple finite distributed lag model is expressed in the form

$y_{t} = {\alpha } + \sum _{i=0}^{p}{{\beta }_{i}x_{t-i}} + {\epsilon }_{t}$

When the lag length (p) is long, severe multicollinearity can occur. Use the Almon or polynomial distributed lag model to avoid this problem, since the relatively low-degree d (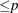 ${{\le } p}$ ) polynomials can capture the true lag distribution. The lag coefficient can be written in the Almon polynomial lag

${\beta }_{i} = {\alpha }_{0}^{*} + \sum _{j=1}^{d}{{\alpha }_{j}^{*} i^{j}}$

Emerson (1968) proposed an efficient method of constructing orthogonal polynomials from the preceding polynomial equation as

${\beta }_{i} = {\alpha }_{0} + \sum _{j=1}^{d}{{\alpha }_{j} f_{j}(i)}$

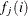where ${f_{j}(i)}$ is a polynomial of degree j in the lag length i. The polynomials 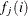${f_{j}(i)}$ are chosen so that they are orthogonal:

$\sum _{i=1}^{n}{w_{i}f_{j}(i)f_{k}(i)} = \begin{cases} 1 & \mr{if} j = k \\ 0 & \mr{if} j {\neq } k \end{cases}$

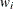where ${w_{\mi{i} }}$ is the weighting factor, and 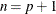${n = p+1 }$ . PROC PDLREG uses the equal weights ( 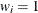${w_{\mi{i} }=1}$ ) for all i. To construct the orthogonal polynomials, the following recursive relation is used:

$f_{j}(i) = (A_{j}i + B_{j})f_{j-1}(i) - C_{j}f_{j-2}(i) j=1,{\ldots }, d$

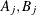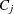The constants ${A_{j}, B_{j}}$ , and ${C_{j}}$ are determined as follows:

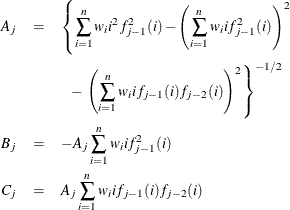
$\begin{eqnarray*} A_{j} & =& \left\{ \sum _{i=1}^{n}{w_{i}i^{2}f_{j-1}^{2}(i)} -\left(\sum _{i=1}^{n}{w_{i}i f_{j-1}^{2}(i)} \right)^{2} \right. \\ & & ~ ~ - \left. \left(\sum _{i=1}^{n}{w_{i}i f_{j-1}(i)f_{j-2}(i)} \right)^{2} \right\} ^{-1/2} \\ B_{j} & =& -A_{j}\sum _{i=1}^{n}{w_{i}i f_{j-1}^{2}(i)} \\ C_{j} & =& A_{j}\sum _{i=1}^{n}{w_{i}i f_{j-1}(i)f_{j-2}(i)} \end{eqnarray*}$

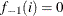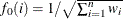where ${f_{-1}(i)=0}$ and ${f_{0}(i)=1/\sqrt {\sum _{i=1}^{n}{w_{i}}} }$ .

PROC PDLREG estimates the orthogonal polynomial coefficients, 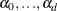${{\alpha }_{0},{\ldots },{\alpha }_{d}}$ , to compute the coefficient estimate of each independent variable (X) with distributed lags. For example, if an independent variable is specified as X(9,3), a third-degree polynomial is used to specify the distributed lag coefficients. The third-degree polynomial is fit as a constant term, a linear term, a quadratic term, and a cubic term. The four terms are constructed to be orthogonal. 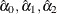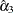In the output produced by the PDLREG procedure for this case, parameter estimates with names X**0, X**1, X**2, and X**3 correspond to ${\hat{{\alpha }}_{0}, \hat{{\alpha }}_{1}, \hat{{\alpha }}_{2}}$ , and ${\hat{{\alpha }}_{3}}$ , respectively. A test using the t statistic and the approximate p-value ("Approx Pr 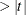$> |t|$ ") associated with X**3 can determine whether a second-degree polynomial rather than a third-degree polynomial is appropriate. The estimates of the 10 lag coefficients associated with the specification X(9,3) are labeled X(0), X(1), X(2), X(3), X(4), X(5), X(6), X(7), X(8), and X(9).