The HPCOPULA Procedure

Student’s t copula

Subsections:

Let $\Theta = \{ (\nu , \Sigma ) : \nu \in (1, \infty ), \Sigma \in \mathbb {R}^{m \times m} \} $, and let $t_\nu $ be a univariate t distribution with $\nu $ degrees of freedom.

The Student’s t copula can be written as

\[ C_{\Theta }(u_1, u_2,{\ldots } u_ m) = \pmb t_{\nu ,\Sigma } \Bigl (t_\nu ^{-1} (u_1), t_\nu ^{-1} (u_2),{\ldots }, t_\nu ^{-1} (u_ m)\Bigr ) \]

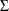where $\pmb t_{\nu ,\Sigma }$ is the multivariate Student’s t distribution that has a correlation matrix $\Sigma $ with $\nu $ degrees of freedom.

Simulation

The input parameters for the simulation are $(\nu , \Sigma )$. The t copula can be simulated by the following steps:

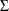  1. Generate a multivariate vector $\bm X \sim t_ m(\nu ,0,\Sigma )$ that follows the centered t distribution with $\nu $ degrees of freedom and correlation matrix $\Sigma $.

  2. Transform the vector $\bm X$ into $\bm U= (t_\nu (X_1),\ldots ,t_\nu (X_ m))^ T$, where $t_\nu $ is the distribution function of univariate t distribution with $\nu $ degrees of freedom.

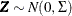To simulate centered multivariate t random variables, you can use the property that $\bm X \sim t_ m(\nu ,0,\Sigma )$ if $\bm X= \sqrt {\nu /s}\bm Z$, where $\bm Z \sim N(0,\Sigma )$ and the univariate random variable $s \sim \chi ^2_\nu $.