The ENTROPY Procedure(Experimental)

Parameter Covariance For GCE-M

Golan, Judge, and Miller (1996) give the finite approximation to the asymptotic variance matrix of the moment formulation as:

\[ \hat{Var}(\hat{\beta })=\Sigma _{z} X’X C^{-1} D C^{-1} X’X \Sigma _{z} \]

where

\[ C=X’X \Sigma _{z} X’X + \Sigma _{v} \]

and

\[ D=X’ \Sigma _{e} X \]

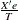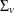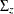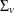Recall that in the moment formulation, V is the support of $\frac{X'e}{T}$, which implies that $\Sigma _{v}$ is a k-dimensional variance matrix. $\Sigma _{z}$ and $\Sigma _{v}$ are both diagonal matrices with the form

\[ \Sigma _{z}=\left[ \begin{array}{ccc} \sum _{l=1}^{L}z_{1l}^{2}p_{1l}-(\sum _{l=1}^{L}z_{1l}p_{1l})^{2} & 0 & 0\\ 0 & \ddots & 0\\ 0 & 0 & \sum _{l=1}^{L}z_{Kl}^{2}p_{Kl}-(\sum _{l=1}^{L}z_{Kl}p_{Kl})^{2}\\ \end{array} \right] \]

and

\[ \Sigma _{v}=\left[ \begin{array}{ccc} \sum _{j=1}^{J}v_{1j}^{2}w_{jl}-(\sum _{j=1}^{J}v_{1j}w_{1j})^{2} & 0 & 0\\ 0 & \ddots & 0\\ 0 & 0 & \sum _{j=1}^{J}v_{Kl}^{2}w_{Kl}-(\sum _{j=1}^{J}v_{Kl}w_{Kl})^{2}\\ \end{array} \right] \]