The STATESPACE Procedure

The State Space Model

The state space model represents a multivariate time series through auxiliary variables, some of which might not be directly observable. These auxiliary variables are called the state vector. The state vector summarizes all the information from the present and past values of the time series that is relevant to the prediction of future values of the series. The observed time series are expressed as linear combinations of the state variables. The state space model is also called a Markovian representation, or a canonical representation, of a multivariate time series process. The state space approach to modeling a multivariate stationary time series is summarized in Akaike (1976).

The state space form encompasses a very rich class of models. Any Gaussian multivariate stationary time series can be written in a state space form, provided that the dimension of the predictor space is finite. In particular, any autoregressive moving average (ARMA) process has a state space representation and, conversely, any state space process can be expressed in an ARMA form (Akaike, 1974). More details on the relation of the state space and ARMA forms are given in the section Relation of ARMA and State Space Forms.

Let ${\mb{x}_{t}}$ be the ${r \times 1}$ vector of observed variables, after differencing (if differencing is specified) and subtracting the sample mean. Let ${\mb{z}_{t}}$ be the state vector of dimension s, $s \geq r$ , where the first r components of ${\mb{z}_{t}}$ consist of ${\mb{x}_{t}}$ . Let the notation ${\mb{x}_{t+k|t}}$ represent the conditional expectation (or prediction) of ${\mb{x}_{t+k}}$ based on the information available at time t. Then the last ${s - r}$ elements of ${\mb{z}_{t}}$ consist of elements of x $_{t+k|t}$ , where k >0 is specified or determined automatically by the procedure.

There are various forms of the state space model in use. The form of the state space model used by the STATESPACE procedure is based on Akaike (1976). The model is defined by the following state transition equation :

$\mb{z}_{t+1} = \mb{F} \mb{z}_{t} + \mb{G} \mb{e}_{t+1}$

In the state transition equation, the ${s \times s}$ coefficient matrix F is called the transition matrix; it determines the dynamic properties of the model.

The ${s \times r}$ coefficient matrix G is called the input matrix; it determines the variance structure of the transition equation. For model identification, the first r rows and columns of G are set to an ${r \times r}$ identity matrix.

The input vector e $_{t}$ is a sequence of independent normally distributed random vectors of dimension r with mean 0 and covariance matrix ${{\Sigma }_{\mb{ee}}}$ . The random error e $_{t}$ is sometimes called the innovation vector or shock vector.

In addition to the state transition equation, state space models usually include a measurement equation or observation equation that gives the observed values ${\mb{x}_{t}}$ as a function of the state vector ${\mb{z}_{t}}$ . However, since PROC STATESPACE always includes the observed values ${\mb{x}_{t}}$ in the state vector ${\mb{z}_{t}}$ , the measurement equation in this case merely represents the extraction of the first r components of the state vector.

The measurement equation used by the STATESPACE procedure is

$\mb{x}_{t} = [ \mb{I}_{r} \mb{0} ] \mb{z}_{t}$

where ${\mb{I}_{r}}$ is an ${r \times r}$ identity matrix. In practice, PROC STATESPACE performs the extraction of ${\mb{x}_{t}}$ from ${\mb{z}_{t}}$ without reference to an explicit measurement equation.

In summary:

x $_{t}$: is an observation vector of dimension r.
z $_{t}$: is a state vector of dimension s, whose first r elements are x $_{t}$ and whose last ${s-r}$ elements are conditional prediction of future x $_{t}$ .
F: is an $\mi{s} {\times }\mi{s}$ transition matrix.
G: is an 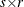$\mi{s} {\times }\mi{r}$ input matrix, with the identity matrix I $_{r}$ forming the first r rows and columns.
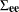e $_{t}$: is a sequence of independent normally distributed random vectors of dimension r with mean 0 and covariance matrix ${{\Sigma }_{\mb{ee}}}$ .