The PDLREG Procedure
The simple finite distributed lag model is expressed in the form
When the lag length (p) is long, severe multicollinearity can occur. Use the Almon or polynomial distributed lag model to avoid this problem, since the relatively low-degree d (![]() ) polynomials can capture the true lag distribution. The lag coefficient can be written in the Almon polynomial lag
) polynomials can capture the true lag distribution. The lag coefficient can be written in the Almon polynomial lag
Emerson (1968) proposed an efficient method of constructing orthogonal polynomials from the preceding polynomial equation as
where ![]() is a polynomial of degree j in the lag length i. The polynomials
is a polynomial of degree j in the lag length i. The polynomials ![]() are chosen so that they are orthogonal:
are chosen so that they are orthogonal:
where ![]() is the weighting factor, and
is the weighting factor, and ![]() . PROC PDLREG uses the equal weights (
. PROC PDLREG uses the equal weights (![]() ) for all i. To construct the orthogonal polynomials, the following recursive relation is used:
) for all i. To construct the orthogonal polynomials, the following recursive relation is used:
The constants ![]() , and
, and ![]() are determined as follows:
are determined as follows:
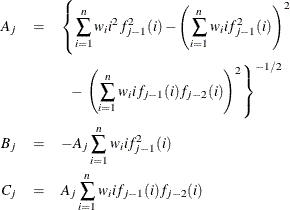
where ![]() and
and ![]() .
.
PROC PDLREG estimates the orthogonal polynomial coefficients, ![]() , to compute the coefficient estimate of each independent variable (X) with distributed lags. For example, if an independent
variable is specified as X(9,3), a third-degree polynomial is used to specify the distributed lag coefficients. The third-degree
polynomial is fit as a constant term, a linear term, a quadratic term, and a cubic term. The four terms are constructed to
be orthogonal. In the output produced by the PDLREG procedure for this case, parameter estimates with names X**0, X**1, X**2,
and X**3 correspond to
, to compute the coefficient estimate of each independent variable (X) with distributed lags. For example, if an independent
variable is specified as X(9,3), a third-degree polynomial is used to specify the distributed lag coefficients. The third-degree
polynomial is fit as a constant term, a linear term, a quadratic term, and a cubic term. The four terms are constructed to
be orthogonal. In the output produced by the PDLREG procedure for this case, parameter estimates with names X**0, X**1, X**2,
and X**3 correspond to ![]() , and
, and ![]() , respectively. A test using the t statistic and the approximate p-value ("Approx Pr
, respectively. A test using the t statistic and the approximate p-value ("Approx Pr ![]() ") associated with X**3 can determine whether a second-degree polynomial rather than a third-degree polynomial is appropriate.
The estimates of the 10 lag coefficients associated with the specification X(9,3) are labeled X(0), X(1), X(2), X(3), X(4),
X(5), X(6), X(7), X(8), and X(9).
") associated with X**3 can determine whether a second-degree polynomial rather than a third-degree polynomial is appropriate.
The estimates of the 10 lag coefficients associated with the specification X(9,3) are labeled X(0), X(1), X(2), X(3), X(4),
X(5), X(6), X(7), X(8), and X(9).
