The MODEL Procedure
This example illustrates how to use SMM to estimate a stochastic volatility model as in Andersen and Sorensen (1996):
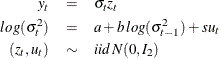
This model is widely used in modeling the return process of stock prices and foreign exchange rates. This is called the stochastic
volatility model because the volatility is stochastic as the random variable ![]() appears in the volatility equation. The following SAS statements use three moments: absolute value, the second-order moment,
and absolute value of the first-order autoregressive moment. Note the ADJSMMV option in the FIT statement to request the SMM
covariance adjustment for the parameter estimates. Although these moments have closed form solution as shown by Andersen and
Sorensen (1996), the simulation approach significantly simplifies the moment conditions.
appears in the volatility equation. The following SAS statements use three moments: absolute value, the second-order moment,
and absolute value of the first-order autoregressive moment. Note the ADJSMMV option in the FIT statement to request the SMM
covariance adjustment for the parameter estimates. Although these moments have closed form solution as shown by Andersen and
Sorensen (1996), the simulation approach significantly simplifies the moment conditions.
%let nobs=1000;
data _tmpdata;
a = -0.736; b=0.9; s=0.363;
ll=sqrt( exp(a/(1-b)));;
do i=-10 to &nobs;
u = rannor( 101 );
z = rannor( 101 );
lnssq = a+b*log(ll**2) +s*u;
st = sqrt(exp(lnssq));
ll = st;
y = st * z;
if i > 0 then output;
end;
run;
title1 'Simulated Method of Moments for Stochastic Volatility Model';
proc model data=_tmpdata ;
parms a b .5 s 1;
instrument / intonly;
u = rannor( 8801 );
z = rannor( 9701 );
lsigmasq = xlag(sigmasq,exp(a));
lnsigmasq = a + b * log(lsigmasq) + s * u;
sigmasq = exp( lnsigmasq );
ysim = sqrt(sigmasq) * z;
eq.m1 = abs(y) - abs(ysim);
eq.m2 = y**2 - ysim**2;
eq.m5 = abs(y*lag(y))-abs(ysim*lag(ysim));
fit m1 m2 m5 / gmm npreobs=10 ndraw=10 adjsmmv;
bound s > 0, 1 > b > 0;
run;
The output of the MODEL procedure is shown in Output 19.17.1.