The MODEL Procedure
This example illustrates how to use SMM to estimate an AR(1) regression model for the following process:
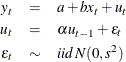
In the following SAS statements, ![]() is simulated by using this model, and the endogenous variable y is set to be equal to
is simulated by using this model, and the endogenous variable y is set to be equal to ![]() . The MOMENT statement creates two more moments for the estimation. One is the second moment, and the other is the first-order
autocovariance. The NPREOBS=10 option instructs PROC MODEL to run the simulation 10 times before
. The MOMENT statement creates two more moments for the estimation. One is the second moment, and the other is the first-order
autocovariance. The NPREOBS=10 option instructs PROC MODEL to run the simulation 10 times before ![]() is compared to the first observation of y. Because the initial
is compared to the first observation of y. Because the initial ![]() is zero, the first
is zero, the first ![]() is
is ![]() . Without the NPREOBS option, this
. Without the NPREOBS option, this ![]() is matched with the first observation of y. With NPREOBS, this
is matched with the first observation of y. With NPREOBS, this ![]() and the next nine
and the next nine ![]() are thrown away, and the moment match starts with the eleventh
are thrown away, and the moment match starts with the eleventh ![]() with the first observation of y. This way, the initial values do not exert a large influence on the simulated endogenous variables.
with the first observation of y. This way, the initial values do not exert a large influence on the simulated endogenous variables.
%let nobs=500;
data ardata;
lu =0;
do i=-10 to &nobs;
x = rannor( 1011 );
e = rannor( 1011 );
u = .6 * lu + 1.5 * e;
Y = 2 + 1.5 * x + u;
lu = u;
if i > 0 then output;
end;
run;
title1 'Simulated Method of Moments for AR(1) Process';
proc model data=ardata ;
parms a b s 1 alpha .5;
instrument x;
u = alpha * zlag(u) + s * rannor( 8003 );
ysim = a + b * x + u;
y = ysim;
moment y = (2) lag1(1);
fit y / gmm npreobs=10 ndraw=10;
bound s > 0, 1 > alpha > 0;
run;
The output of the MODEL procedure is shown in Output 19.16.1: