The SEVERITY Procedure
- Overview
-
Getting Started

-
Syntax

-
Details
 Predefined DistributionsCensoring and TruncationParameter Estimation MethodParameter InitializationEstimating Regression EffectsEmpirical Distribution Function Estimation MethodsStatistics of FitDefining a Distribution Model with the FCMP ProcedurePredefined Utility FunctionsScoring FunctionsCustom Objective FunctionsMultithreaded ComputationInput Data SetsOutput Data SetsDisplayed OutputODS Graphics
Predefined DistributionsCensoring and TruncationParameter Estimation MethodParameter InitializationEstimating Regression EffectsEmpirical Distribution Function Estimation MethodsStatistics of FitDefining a Distribution Model with the FCMP ProcedurePredefined Utility FunctionsScoring FunctionsCustom Objective FunctionsMultithreaded ComputationInput Data SetsOutput Data SetsDisplayed OutputODS Graphics -
Examples
 Defining a Model for Gaussian DistributionDefining a Model for Gaussian Distribution with a Scale ParameterDefining a Model for Mixed-Tail DistributionsEstimating Parameters Using Cramér-von Mises EstimatorFitting a Scaled Tweedie Model with RegressorsFitting Distributions to Interval-Censored DataDefining a Finite Mixture Model That Has a Scale ParameterPredicting Mean and Value-at-Risk by Using Scoring Functions
Defining a Model for Gaussian DistributionDefining a Model for Gaussian Distribution with a Scale ParameterDefining a Model for Mixed-Tail DistributionsEstimating Parameters Using Cramér-von Mises EstimatorFitting a Scaled Tweedie Model with RegressorsFitting Distributions to Interval-Censored DataDefining a Finite Mixture Model That Has a Scale ParameterPredicting Mean and Value-at-Risk by Using Scoring Functions - References
One of the key features of PROC SEVERITY is that it enables you to specify whether the severity event’s magnitude is observable and if it is observable, then whether the exact value of the magnitude is known. If an event is unobservable when the magnitude is in certain intervals, then it is referred to as a truncation effect. If the exact magnitude of the event is not known, but it is known to have a value in a certain interval, then it is referred to as a censoring effect.
PROC SEVERITY allows a severity event to be subject to any combination of the following four censoring and truncation effects:
-
Left-truncation: An event is said to be left-truncated if it is observed only when
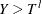 , where
, where 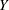 denotes the random variable for the magnitude and
denotes the random variable for the magnitude and 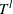 denotes a random variable for the truncation threshold. You can specify left-truncation using the LEFTTRUNCATED= option in the LOSS statement.
denotes a random variable for the truncation threshold. You can specify left-truncation using the LEFTTRUNCATED= option in the LOSS statement.
-
Right-truncation: An event is said to be right-truncated if it is observed only when
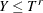 , where
, where 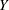 denotes the random variable for the magnitude and
denotes the random variable for the magnitude and 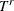 denotes a random variable for the truncation threshold. You can specify right-truncation using the RIGHTTRUNCATED= option in the LOSS statement.
denotes a random variable for the truncation threshold. You can specify right-truncation using the RIGHTTRUNCATED= option in the LOSS statement.
-
Left-censoring: An event is said to be left-censored if it is known that the magnitude is
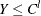 , but the exact value of
, but the exact value of 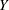 is not known.
is not known. 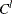 is a random variable for the censoring limit. You can specify left-censoring using the LEFTCENSORED= option in the LOSS statement.
is a random variable for the censoring limit. You can specify left-censoring using the LEFTCENSORED= option in the LOSS statement.
-
Right-censoring: An event is said to be right-censored if it is known that the magnitude is
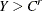 , but the exact value of
, but the exact value of 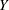 is not known.
is not known. 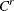 is a random variable for the censoring limit. You can specify right-censoring using the RIGHTCENSORED= option in the LOSS statement.
is a random variable for the censoring limit. You can specify right-censoring using the RIGHTCENSORED= option in the LOSS statement.
For each effect, you can specify a different threshold or limit for each observation or specify a single threshold or limit that applies to all the observations.
If all the four types of effects are present on an event, then the following relationship holds: ![]() . PROC SEVERITY checks these relationships and write a warning to the SAS log if any is violated.
. PROC SEVERITY checks these relationships and write a warning to the SAS log if any is violated.
If you specify the response variable in the LOSS statement, then PROC SEVERITY also checks whether each observation satisfies
the definitions of the specified censoring and truncation effects. If you specify left-truncation, then PROC SEVERITY ignores
observations where ![]() , because such observations are not observable by definition. Similarly, if you specify right-truncation, then PROC SEVERITY
ignores observations where
, because such observations are not observable by definition. Similarly, if you specify right-truncation, then PROC SEVERITY
ignores observations where ![]() . If you specify left-censoring, then PROC SEVERITY treats an observation with
. If you specify left-censoring, then PROC SEVERITY treats an observation with ![]() as uncensored and ignores the value of
as uncensored and ignores the value of ![]() . The observations with
. The observations with ![]() are considered as left-censored, and the value of
are considered as left-censored, and the value of ![]() is ignored. If you specify right-censoring, then PROC SEVERITY treats an observation with
is ignored. If you specify right-censoring, then PROC SEVERITY treats an observation with ![]() as uncensored and ignores the value of
as uncensored and ignores the value of ![]() . The observations with
. The observations with ![]() are considered as right-censored, and the value of
are considered as right-censored, and the value of ![]() is ignored. If you specify both left-censoring and right-censoring, it is referred to as interval-censoring. If
is ignored. If you specify both left-censoring and right-censoring, it is referred to as interval-censoring. If ![]() is satisfied for an observation, then it is considered as interval-censored and the value of the response variable is ignored.
If
is satisfied for an observation, then it is considered as interval-censored and the value of the response variable is ignored.
If ![]() for an observation, then PROC SEVERITY assumes that observation to be uncensored. If all the observations in a data set are
censored in some form, then the specification of the response variable in the LOSS statement is optional, because the actual
value of the response variable is not required for the purposes of estimating a model.
for an observation, then PROC SEVERITY assumes that observation to be uncensored. If all the observations in a data set are
censored in some form, then the specification of the response variable in the LOSS statement is optional, because the actual
value of the response variable is not required for the purposes of estimating a model.
Specification of censoring and truncation affects the likelihood of the data (see the section Likelihood Function) and how the empirical distribution function (EDF) is estimated (see the section Empirical Distribution Function Estimation Methods).
For left-truncated data, PROC SEVERITY also enables you to provide additional information in the form of probability of observability by using the PROBOBSERVED= option. It is defined as the probability that the underlying severity event gets observed (and recorded) for the specified left-truncation threshold value. For example, if you specify a value of 0.75, then for every 75 observations recorded above a specified threshold, 25 more events have happened with a severity value less than or equal to the specified threshold. Although the exact severity value of those 25 events is not known, PROC SEVERITY can use the information about the number of those events.
In particular, for each left-truncated observation, PROC SEVERITY assumes a presence of ![]() additional observations with
additional observations with ![]() . These additional observations are then used for computing the likelihood (see the section Probability of Observability and Likelihood) and an unconditional estimate of the empirical distribution function (see the section EDF Estimates and Truncation).
. These additional observations are then used for computing the likelihood (see the section Probability of Observability and Likelihood) and an unconditional estimate of the empirical distribution function (see the section EDF Estimates and Truncation).
If you specify left-truncation without the probability of observability or if you specify right-truncation, then the EDF estimates that are computed by all methods except the STANDARD method are conditional on the truncation information. See the section EDF Estimates and Truncation for more information. In such cases, PROC SEVERITY uses conditional estimates of the CDF whenever they are used for computational or visual comparison with the EDF estimates.
Let ![]() be the smallest value of the left-truncation threshold (
be the smallest value of the left-truncation threshold (![]() is the left-truncation threshold for observation
is the left-truncation threshold for observation ![]() ) and
) and ![]() be the largest value of the right-truncation threshold (
be the largest value of the right-truncation threshold (![]() is the right-truncation threshold for observation
is the right-truncation threshold for observation ![]() ). If
). If ![]() denotes the unconditional estimate of the CDF at
denotes the unconditional estimate of the CDF at ![]() , then the conditional estimate
, then the conditional estimate ![]() is computed as follows:
is computed as follows:
-
If you do not specify the probability of observability, then the EDF estimates are conditional on the left-truncation information. If an observation is both left-truncated and right-truncated, then
![\[ \hat{F}^ c(y) = \frac{\hat{F}(y) - \hat{F}(t^ l_{\text {min}})}{\hat{F}(t^ r_{\text {max}}) - \hat{F}(t^ l_{\text {min}})} \]](images/etsug_severity0249.png)
If an observation is left-truncated but not right-truncated, then
![\[ \hat{F}^ c(y) = \frac{\hat{F}(y) - \hat{F}(t^ l_{\text {min}})}{1 - \hat{F}(t^ l_{\text {min}})} \]](images/etsug_severity0250.png)
If an observation is right-truncated but not left-truncated, then
![\[ \hat{F}^ c(y) = \frac{\hat{F}(y)}{\hat{F}(t^ r_{\text {max}})} \]](images/etsug_severity0251.png)
-
If you specify the probability of observability, then EDF estimates are not conditional on the left-truncation information. If an observation is not right-truncated, then the conditional estimate is the same as the unconditional estimate. If an observation is right-truncated, then the conditional estimate is computed as
![\[ \hat{F}^ c(y) = \frac{\hat{F}(y)}{\hat{F}(t^ r_{\text {max}})} \]](images/etsug_severity0251.png)
If you specify regressors, then ![]() ,
, ![]() , and
, and ![]() are all computed from a mixture distribution, as described in the section CDF and PDF Estimates with Regression Effects.
are all computed from a mixture distribution, as described in the section CDF and PDF Estimates with Regression Effects.