The PANEL Procedure
- Overview
-
Getting Started

-
Syntax

-
Details
 Missing ValuesComputational ResourcesRestricted EstimatesNotationOne-Way Fixed-Effects ModelTwo-Way Fixed-Effects ModelBalanced PanelsUnbalanced PanelsBetween EstimatorsPooled EstimatorOne-Way Random-Effects ModelTwo-Way Random-Effects ModelParks Method (Autoregressive Model)Da Silva Method (Variance-Component Moving Average Model)Dynamic Panel EstimatorLinear Hypothesis TestingHeteroscedasticity-Corrected Covariance MatricesHeteroscedasticity- and Autocorrelation-Consistent Covariance MatricesR SquareSpecification TestsPanel Data Poolability TestPanel Data Unit Root TestsTroubleshootingCreating ODS GraphicsOUTPUT OUT= Data SetOUTEST= Data SetOUTTRANS= Data SetPrinted OutputODS Table Names
Missing ValuesComputational ResourcesRestricted EstimatesNotationOne-Way Fixed-Effects ModelTwo-Way Fixed-Effects ModelBalanced PanelsUnbalanced PanelsBetween EstimatorsPooled EstimatorOne-Way Random-Effects ModelTwo-Way Random-Effects ModelParks Method (Autoregressive Model)Da Silva Method (Variance-Component Moving Average Model)Dynamic Panel EstimatorLinear Hypothesis TestingHeteroscedasticity-Corrected Covariance MatricesHeteroscedasticity- and Autocorrelation-Consistent Covariance MatricesR SquareSpecification TestsPanel Data Poolability TestPanel Data Unit Root TestsTroubleshootingCreating ODS GraphicsOUTPUT OUT= Data SetOUTEST= Data SetOUTTRANS= Data SetPrinted OutputODS Table Names -
Example

- References
For a linear hypothesis of the form R ![]() where
where ![]() is
is ![]() and
and ![]() is
is ![]() , the
, the ![]() -statistic with
-statistic with ![]() degrees of freedom is computed as
degrees of freedom is computed as
However, it is also possible to write the ![]() statistic as
statistic as
where
-
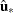 is the residual vector from the restricted regression
is the residual vector from the restricted regression
-
 is the residual vector from the unrestricted regression
is the residual vector from the unrestricted regression
-
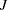 is the number of restrictions
is the number of restrictions
-
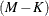 are the degrees of freedom,
are the degrees of freedom, 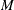 is the number of observations, and
is the number of observations, and 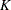 is the number of parameters in the model
is the number of parameters in the model
The Wald, likelihood ratio (LR) and Lagrange multiplier (LM) tests are all related to the ![]() test. You use this relationship of the
test. You use this relationship of the ![]() test to the likelihood ratio and Lagrange multiplier tests. The Wald test is calculated from its definition.
test to the likelihood ratio and Lagrange multiplier tests. The Wald test is calculated from its definition.
The Wald test statistic is:
The advantage of calculating Wald in this manner is that it enables you to substitute a heteroscedasticity-corrected covariance
matrix for the matrix ![]() . PROC PANEL makes such a substitution if you request the HCCME option in the MODEL statement.
. PROC PANEL makes such a substitution if you request the HCCME option in the MODEL statement.
The likelihood ratio is:
The Lagrange multiplier test statistic is:
where JF represents the number of restrictions multiplied by the result of the ![]() test.
test.
Note that only the Wald is changed when the HCCME option is selected. The LR and LM tests are unchanged.
The distribution of these test statistics is the ![]() with degrees of freedom equal to the number of restrictions imposed (
with degrees of freedom equal to the number of restrictions imposed (![]() ). The three tests are asymptotically equivalent, but they have differing small sample properties. Greene (2000, p. 392) and
Davidson and MacKinnon (1993, pg. 456-458) discuss the small sample properties of these statistics.
). The three tests are asymptotically equivalent, but they have differing small sample properties. Greene (2000, p. 392) and
Davidson and MacKinnon (1993, pg. 456-458) discuss the small sample properties of these statistics.