Model Fit and Goodness-of-Fit Statistics :: SAS/ETS(R) 12.3 User's Guide

Model Fit and Goodness-of-Fit Statistics

McFadden (1974) suggests a likelihood ratio index that is analogous to the R-square in the linear regression model:

$R^{2}_{M} = 1 - \frac{\ln L}{\ln L_{0}}$

where is the maximum of the log-likelihood function and $L_{0}$ is the maximum of the log-likelihood function when all coefficients, except for an intercept term, are zero. McFadden’s likelihood ratio index is bounded by 0 and 1.

Estrella (1998) proposes the following requirements for a goodness-of-fit measure to be desirable in discrete choice modeling:

The measure must take values in , where 0 represents no fit and 1 corresponds to perfect fit.
The measure should be directly related to the valid test statistic for the significance of all slope coefficients.
The derivative of the measure with respect to the test statistic should comply with corresponding derivatives in a linear regression.

Estrella’s measure is written as

$R_{E1}^{2} = 1 - \left(\frac{\ln L}{\ln L_{0}}\right) ^{-(2 / N) \ln L_{0}}$

Estrella suggests an alternative measure,

$R_{E2}^{2} = 1 - [ (\ln L - K) / \ln L_{0} ]^{-(2 / N) \ln L_{0}}$

where $\ln L_{0}$ is computed with null parameter values, is the number of observations used, and represents the number of estimated parameters.

Other goodness-of-fit measures are summarized as follows:

$\displaystyle R_{CU1}^{2}$	$\displaystyle = 1 - \left(\frac{L_{0}}{L}\right)^{\frac{2}{N}} \; \;$	$\displaystyle (\textrm{Cragg-Uhler 1})$
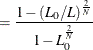$\displaystyle R_{CU2}^{2}$	$\displaystyle = \frac{1 - (L_{0}/L)^{\frac{2}{N}}}{1 - L_{0}^{\frac{2}{N}}} \; \;$	$\displaystyle (\textrm{Cragg-Uhler 2})$
$\displaystyle R_{A}^{2}$	$\displaystyle = \frac{2(\ln L - \ln L_{0})}{2(\ln L - \ln L_{0})+N} \; \;$	$\displaystyle (\textrm{Aldrich-Nelson})$
$\displaystyle R_{VZ}^{2}$	$\displaystyle = R_{A}^{2}\frac{2\ln L_{0} - N}{2\ln L_{0}} \; \;$	$\displaystyle (\textrm{Veall-Zimmermann})$

The AIC and SBC are computed as follows:

$AIC = -2\; ln(L)+2\; k$

$SBC = -2\; ln(L)+ln(n)\; k$

where is the log-likelihood value for the model, is the number of parameters estimated, and is the number of observations (that is, the number of respondents).