PROC ENTROPY Statement :: SAS/ETS(R) 12.3 User's Guide

General Options

COLLIN: requests that the collinearity diagnostics of the 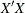matrix be printed.
COVBEST=CROSS | GME | GMEM: specifies the method for producing the covariance matrix of parameters for output and for standard error calculations. GMEM and GME are aliases and are the default.
GME | GCE: requests generalized maximum entropy or generalized cross entropy. This is the default estimation method.
GMEM | GCEM: requests moment maximum entropy or the moment cross entropy.
GMED: requests a variant of GME suitable for multinomial discrete choice models.
MARKOV: specifies that the model is a first-order Markov model.
PURE: specifies a regression without an error term.
SUR | ITSUR: specifies seemingly unrelated regression or iterated seemingly unrelated regression.
VARDEF=N | WGT | DF | WDF: specifies the denominator to be used in computing variances and covariances. VARDEF=N specifies that the number of nonmissing observations be used. VARDEF=WGT specifies that the sum of the weights be used. VARDEF=DF specifies that the number of nonmissing observations minus the model degrees of freedom (number of parameters) be used. VARDEF=WDF specifies that the sum of the weights minus the model degrees of freedom be used. The default is VARDEF=DF.

Data Set Options

DATA=SAS-data-set: specifies the input data set. Values for the variables in the model are read from this data set.
PDATA=SAS-data-set: names the SAS data set that contains the data about priors and supports.
OUT=SAS-data-set: names the SAS data set to contain the residuals from each estimation.
OUTCOV
COVOUT: writes the covariance matrix of the estimates to the OUTEST= data set in addition to the parameter estimates. The OUTCOV option is applicable only if the OUTEST= option is also specified.
OUTEST=SAS-data-set: names the SAS data set to contain the parameter estimates and optionally the covariance of the estimates.
OUTL=SAS-data-set: names the SAS data set to contain the estimated Lagrange multipliers for the models.
OUTP=SAS-data-set: names the SAS data set to contain the support points and estimated probabilities.
OUTS=SAS-data-set: names the SAS data set to contain the estimated covariance matrix of the equation errors. This is the covariance of the residuals computed from the parameter estimates.
OUTSUSED=SAS-data-set: names the SAS data set to contain the 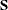$\mb {S}$ matrix used in the objective function definition. The OUTSUSED= data set is the same as the OUTS= data set for the methods that iterate the 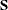$\mb {S}$ matrix.
SDATA=SAS-data-set: specifies a data set that provides the covariance matrix of the equation errors. The matrix read from the SDATA= data set is used for the equation error covariance matrix (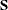 $\mb {S}$ matrix) in the estimation. The SDATA= matrix is used to provide only the initial estimate of 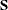$\mb {S}$ for the methods that iterate the S matrix.

Printing Options

ITPRINT

prints the parameter estimates, objective function value, and convergence criteria at each iteration.

NOPRINT

suppresses the normal printed output but does not suppress error listings. Using any other print option turns the NOPRINT option off.

PLOTS=global-plot-options | plot-request

controls the plots that the ENTROPY procedure produces. (For general information about ODS Graphics, see Chapter 21: Statistical Graphics Using ODS in SAS/STAT 12.3 User's Guide.) The global-plot-options apply to all relevant plots generated by the ENTROPY procedure.

The global-plot-options supported by the ENTROPY procedure are as follows:

ONLY: suppresses the default plots. Only the plots specifically requested are produced.
UNPACKPANEL: displays each graph separately. (By default, some graphs can appear together in a single panel.)

The specific plot-request values supported by the ENTROPY procedure are as follows:

ALL: requests that all plots appropriate for the particular analysis be produced. ALL is equivalent to specifying FITPLOT, COOKSD, QQ, RESIDUALHISTOGRAM, and STUDENTRESIDUAL.
FITPLOT: plots the predicted and actual values.
COOKSD: produces the Cook’s D plot.
QQ: produces a Q-Q plot of residuals.
RESIDUALHISTOGRAM: plots the histogram of residuals.
STUDENTRESIDUAL: plots the studentized residuals.
NONE: suppresses all plots.

The default behavior is to plot all plots appropriate for the particular analysis (ALL) in a panel.

Options to Control the Minimization Process

The following options can be helpful if a convergence problem occurs for a given model and set of data. The ENTROPY procedure uses the nonlinear optimization subsystem (NLO) to perform the model optimizations. In addition to the options listed below, all options supported in the NLO subsystem can be specified on the ENTROPY procedure statement. See Chapter 6: Nonlinear Optimization Methods, for more details.

CONVERGE=value GCONV=value: specifies the convergence criteria for S-iterated methods. The convergence measure computed during model estimation must be less than value before convergence is assumed. The default value is CONVERGE=0.001.
DUAL | PRIMAL: specifies whether the optimization problem is solved using the dual or primal form. The dual form is the default.
MAXITER=n: specifies the maximum number of iterations allowed. The default is MAXITER=100.
MAXSUBITER=n: specifies the maximum number of subiterations allowed for an iteration. The MAXSUBITER= option limits the number of step halvings. The default is MAXSUBITER=30.
METHOD=TR | NEWRAP | NRR | QN | CONGR | NSIMP | DBLDOG | LEVMAR TECHNIQUE=TR | NEWRAP | NRR | QN | CONGR | NSIMP | DBLDOG | LEVMAR TECH=TR | NEWRAP | NRR | QN | CONGR | NSIMP | DBLDOG | LEVMAR: specifies the iterative minimization method to use. METHOD=TR specifies the trust region method, METHOD=NEWRAP specifies the Newton-Raphson method, METHOD=NRR specifies the Newton-Raphson ridge method, and METHOD=QN specifies the quasi-Newton method. See Chapter 6: Nonlinear Optimization Methods, for more details about optimization methods. The default is METHOD=QN for the dual form and METHOD=NEWRAP for the primal form.

The ENTROPY Procedure (Experimental)