Kernels :: SAS/ETS(R) 12.1 User's Guide

Kernels

Kernels are used to smooth the periodogram by using a weighted moving average of nearby points. A smoothed periodogram is defined by the following equation.

$\displaystyle \hat{J}_{i}(\textrm{l}(q)) = \sum _{{\tau } = -\textrm{l}(q)}^{\textrm{l}(q)} {\textrm{w}\left( \frac{{\tau }}{\textrm{l}(q)} \right) \tilde{J}_{i+{\tau }}} \nonumber$

where ${\mr {w}(x)}$ is the kernel or weight function. At the endpoints, the moving average is computed cyclically; that is,

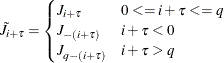$\displaystyle \tilde{J}_{i+{\tau }} = \begin{cases} J_{i+{\tau }} & 0 <= i+\tau <= q \\ J_{-(i+{\tau })} & i+\tau < 0 \\ J_{q-(i+{\tau })} & i+\tau > q \end{cases}\nonumber$

The SPECTRA procedure supports the following kernels. They are listed with their default bandwidth functions.

Bartlett: KERNEL BART

$\displaystyle \textrm{w}(x)$	$\displaystyle =$	$\displaystyle \begin{cases} 1-{\|x\|} & {\|x\|}{\le }1 \\ 0 & \mr {otherwise} \end{cases}$
$\displaystyle \mr {l}(q)$	$\displaystyle =$	$\displaystyle \frac{1}{2} q^{1 / 3} \nonumber$

Parzen: KERNEL PARZEN

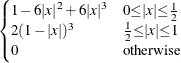$\displaystyle \textrm{w}(x)$	$\displaystyle =$	$\displaystyle \begin{cases} 1-6{\|x\|}^{2} + 6{\|x\|}^{3} & {0{\le }{\|x\|}{\le }\frac{1}{2}} \\ 2(1-{\|x\|})^{3} & {\frac{1}{2}{\le }{\|x\|}{\le }1} \\ 0 & \mr {otherwise} \end{cases}$
$\displaystyle \mr {l}(q)$	$\displaystyle =$	$\displaystyle q^{1 / 5} \nonumber$

Quadratic spectral: KERNEL QS

$\displaystyle \mr {w}(x)$	$\displaystyle =$	$\displaystyle \frac{25}{12{\pi }^{2} x^{2}} \left( \frac{{sin}(6{\pi }x/5)}{6{\pi }x/5} - {cos}(6{\pi }x/5) \right)$
$\displaystyle \textrm{l}(q)$	$\displaystyle =$	$\displaystyle \frac{1}{2} q^{1 / 5} \nonumber$

Tukey-Hanning: KERNEL TUKEY

$\displaystyle \textrm{w}(x)$	$\displaystyle =$	$\displaystyle \begin{cases} (1+{cos}( {\pi } x))/2 & {\|x\|}{\le }1 \\ 0 & \mr {otherwise} \end{cases}$
$\displaystyle \mr {l}(q)$	$\displaystyle =$	$\displaystyle \frac{2}{3} q^{1 / 5} \nonumber$

Truncated: KERNEL TRUNCAT

$\displaystyle \textrm{w}(x)$	$\displaystyle =$	$\displaystyle \begin{cases} 1 & {\|x\|}{\le }1 \\ 0 & \mr {otherwise} \end{cases}$
$\displaystyle \mr {l}(q)$	$\displaystyle =$	$\displaystyle \frac{1}{4} q^{1 / 5} \nonumber$

A summary of the default values of the bandwidth parameters, c and e, associated with the kernel smoothers in PROC SPECTRA are listed below in Table 26.2:

Table 26.2: Bandwidth Parameters

Kernel	c	e
Bartlett
Parzen
quadratic
Tukey-Hanning
truncated

Figure 26.1: Kernels for Smoothing

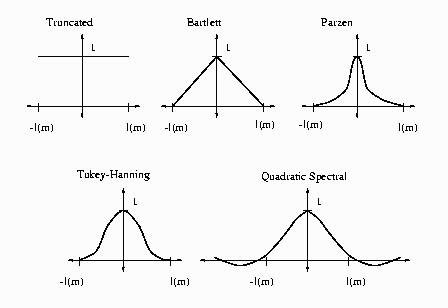
See Andrews (1991) for details about the properties of these kernels.

The SPECTRA Procedure

Kernels