There are several optimization techniques available. You can choose a particular optimizer with the TECH= option in the PROC statement or NLOPTIONS statement.

No algorithm for optimizing general nonlinear functions exists that always finds the global optimum for a general nonlinear minimization problem in a reasonable amount of time. Since no single optimization technique is invariably superior to others, NLO provides a variety of optimization techniques that work well in various circumstances. However, you can devise problems for which none of the techniques in NLO can find the correct solution. Moreover, nonlinear optimization can be computationally expensive in terms of time and memory, so you must be careful when matching an algorithm to a problem.

All optimization techniques in NLO use memory except the conjugate gradient methods, which use only 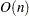of memory and are designed to optimize problems with many parameters. These iterative techniques require repeated computation of the following:

• the function value (optimization criterion)

• the gradient vector (first-order partial derivatives)

• for some techniques, the (approximate) Hessian matrix (second-order partial derivatives)

However, since each of the optimizers requires different derivatives, some computational efficiencies can be gained. Table 6.4 shows, for each optimization technique, which derivatives are required. (FOD means that first-order derivatives or the gradient is computed; SOD means that second-order derivatives or the Hessian is computed.)

Each optimization method employs one or more convergence criteria that determine when it has converged. The various termination criteria are listed and described in the previous section. An algorithm is considered to have converged when any one of the convergence criterion is satisfied. For example, under the default settings, the QUANEW algorithm will converge if , , or .