Example 19.18 Duration Data Model with Unobserved Heterogeneity
All of the previous three models actually have closed-form moment conditions, so the simulation approach is not necessarily required for the estimation. This example illustrates how to use SMM to estimate a model for which there is no closed-form solution for the moments and thus the traditional GMM method does not apply. The model is the duration data model with unobserved heterogeneity in Gourieroux and Monfort (1993):
 |
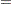 |
 |
|||
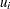 |
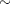 |
 |
The SAS statements are:
title1 'SMM for Duration Model with Unobserved Heterogeneity';
%let nobs=1000;
data durationdata;
b=0.9; s=0.5;
do i=1 to &nobs;
u = rannor( 1011 );
v = ranuni( 1011 );
x = 2 * ranuni( 1011 );
y = -exp(-b * x + s * u) * log(v);
output;
end;
run;
proc model data=durationdata;
parms b .5 s 1;
instrument x;
u = rannor( 1011 );
v = ranuni( 1011 );
y = -exp(-b * x + s * u) * log(v);
moment y = (2 3 4);
fit y / gmm ndraw=10 ;* maxiter=500;
bound s > 0, b > 0;
run;
The output of the MODEL procedure is shown in Output 19.18.1.
Output 19.18.1
PROC MODEL Output
| SMM for Duration Model with Unobserved Heterogeneity |
The MODEL Procedure
| Model Summary | |
|---|---|
| Model Variables | 1 |
| Parameters | 2 |
| Equations | 4 |
| Number of Statements | 9 |
| Model Variables | y |
|---|---|
| Parameters(Value) | b(0.5) s(1) |
| Equations | _moment_3 _moment_2 _moment_1 y |
| The 4 Equations to Estimate | |
|---|---|
| _moment_3 = | F(b, s) |
| _moment_2 = | F(b, s) |
| _moment_1 = | F(b, s) |
| y = | F(b, s) |
| Instruments | 1 x |
| Nonlinear GMM Parameter Estimates | ||||
|---|---|---|---|---|
| Parameter | Estimate | Approx Std Err | t Value | Approx Pr > |t| |
| b | 0.92983 | 0.0331 | 28.08 | <.0001 |
| s | 0.341825 | 0.0608 | 5.62 | <.0001 |