The COUNTREG Procedure
- Overview
- Getting Started
-
Syntax
-
Details
Specification of Regressors Missing Values Poisson Regression Negative Binomial Regression Zero-Inflated Count Regression Overview Zero-Inflated Poisson Regression Zero-Inflated Negative Binomial Regression Computational Resources Nonlinear Optimization Options Covariance Matrix Types Displayed Output OUTPUT OUT= Data Set OUTEST= Data Set ODS Table Names
-
Examples
- References
| Zero-Inflated Poisson Regression |
In the zero-inflated Poisson (ZIP) regression model, the data generation process referred to earlier as Process 2 is
 |
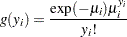where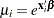 
. Thus the ZIP model is defined as
 |
 |
 |
|||
 |
|
 |
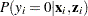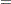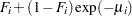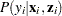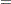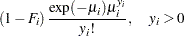The conditional expectation and conditional variance of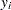 
are given by
 |
 |
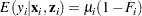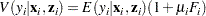Note that the ZIP model (as well as the ZINB model) exhibits overdispersion since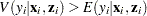 
.
In general, the log-likelihood function of the ZIP model is
 |
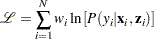After a specific link function (either logistic or standard normal) for the probability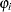 
is chosen, it is possible to write the exact expressions for the log-likelihood function and the gradient.
ZIP Model with Logistic Link Function
First, consider the ZIP model in which the probability 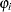is expressed with a logistic link function—namely,
 |
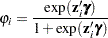The log-likelihood function is
 |
 |
 |
|||
 |
|
 |
|||
|
|
 |
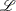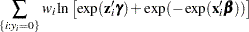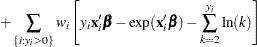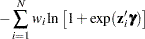See Poisson Regression for the definition of 
.
The gradient for this model is given by
 |
 |
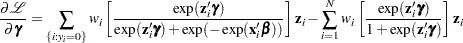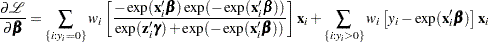ZIP Model with Standard Normal Link Function
Next, consider the ZIP model in which the probability 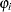is expressed with a standard normal link function: 
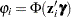. The log-likelihood function is
|
|
 |
|||
|
 |
 |
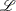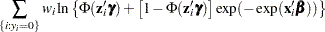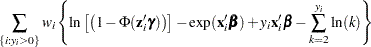See Poisson Regression for the definition of .
The gradient for this model is given by
 |
|
 |
|||
|
 |
 |
 |
|
 |
|||
|
|
 |
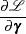
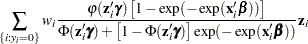
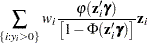
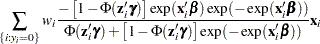
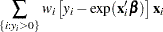