| The X12 Procedure |
Example 34.1 ARIMA Model Identification
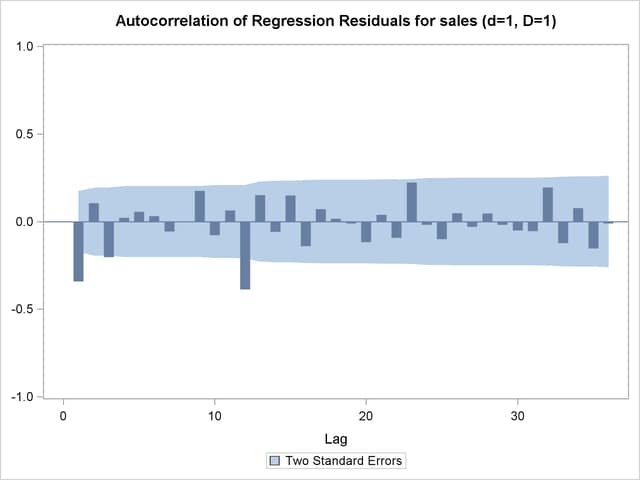
An example of the statements typically invoked when using PROC X12 for ARIMA model identification might follow the same format as the following example. This example invokes the X12 procedure and uses the TRANSFORM and IDENTIFY statements. It specifies the time series data, takes the logarithm of the series (TRANSFORM statement), and generates ACFs and PACFs for the specified levels of differencing (IDENTIFY statement). The ACFs and PACFs for DIFF=1 and SDIFF=1 are shown in Output 34.1.1, Output 34.1.2, Output 34.1.3, and Output 34.1.4. The data set is the same as in the section Basic Seasonal Adjustment.
The graphical displays are requested by specifying the ODS GRAPHICS ON statement. For more information about the graphics available in the X12 procedure, see the section ODS Graphics.
ods graphics on; proc x12 data=sales date=date; var sales; transform power=0; identify diff=(0,1) sdiff=(0,1); run;
| Autocorrelation of Regression Residuals for ARIMA Model Identification | |||||
|---|---|---|---|---|---|
| For Variable sales | |||||
| Differencing: Nonseasonal Order=1 Seasonal Order=1 | |||||
| Lag | Correlation | Standard Error | Chi-Square | DF | Pr > ChiSq |
| 1 | -0.34112 | 0.08737 | 15.5957 | 1 | <.0001 |
| 2 | 0.10505 | 0.09701 | 17.0860 | 2 | 0.0002 |
| 3 | -0.20214 | 0.09787 | 22.6478 | 3 | <.0001 |
| 4 | 0.02136 | 0.10101 | 22.7104 | 4 | 0.0001 |
| 5 | 0.05565 | 0.10104 | 23.1387 | 5 | 0.0003 |
| 6 | 0.03080 | 0.10128 | 23.2709 | 6 | 0.0007 |
| 7 | -0.05558 | 0.10135 | 23.7050 | 7 | 0.0013 |
| 8 | -0.00076 | 0.10158 | 23.7050 | 8 | 0.0026 |
| 9 | 0.17637 | 0.10158 | 28.1473 | 9 | 0.0009 |
| 10 | -0.07636 | 0.10389 | 28.9869 | 10 | 0.0013 |
| 11 | 0.06438 | 0.10432 | 29.5887 | 11 | 0.0018 |
| 12 | -0.38661 | 0.10462 | 51.4728 | 12 | <.0001 |
| 13 | 0.15160 | 0.11501 | 54.8664 | 13 | <.0001 |
| 14 | -0.05761 | 0.11653 | 55.3605 | 14 | <.0001 |
| 15 | 0.14957 | 0.11674 | 58.7204 | 15 | <.0001 |
| 16 | -0.13894 | 0.11820 | 61.6452 | 16 | <.0001 |
| 17 | 0.07048 | 0.11944 | 62.4045 | 17 | <.0001 |
| 18 | 0.01563 | 0.11975 | 62.4421 | 18 | <.0001 |
| 19 | -0.01061 | 0.11977 | 62.4596 | 19 | <.0001 |
| 20 | -0.11673 | 0.11978 | 64.5984 | 20 | <.0001 |
| 21 | 0.03855 | 0.12064 | 64.8338 | 21 | <.0001 |
| 22 | -0.09136 | 0.12074 | 66.1681 | 22 | <.0001 |
| 23 | 0.22327 | 0.12126 | 74.2099 | 23 | <.0001 |
| 24 | -0.01842 | 0.12436 | 74.2652 | 24 | <.0001 |
| 25 | -0.10029 | 0.12438 | 75.9183 | 25 | <.0001 |
| 26 | 0.04857 | 0.12500 | 76.3097 | 26 | <.0001 |
| 27 | -0.03024 | 0.12514 | 76.4629 | 27 | <.0001 |
| 28 | 0.04713 | 0.12520 | 76.8387 | 28 | <.0001 |
| 29 | -0.01803 | 0.12533 | 76.8943 | 29 | <.0001 |
| 30 | -0.05107 | 0.12535 | 77.3442 | 30 | <.0001 |
| 31 | -0.05377 | 0.12551 | 77.8478 | 31 | <.0001 |
| 32 | 0.19573 | 0.12569 | 84.5900 | 32 | <.0001 |
| 33 | -0.12242 | 0.12799 | 87.2543 | 33 | <.0001 |
| 34 | 0.07775 | 0.12888 | 88.3401 | 34 | <.0001 |
| 35 | -0.15245 | 0.12924 | 92.5584 | 35 | <.0001 |
| 36 | -0.01000 | 0.13061 | 92.5767 | 36 | <.0001 |
| Note: | The P-values approximate the probability of observing a Q-value at least this large when the model fitted is correct. When DF is positive, small values of P, customarily those below 0.05 indicate model inadequacy. |
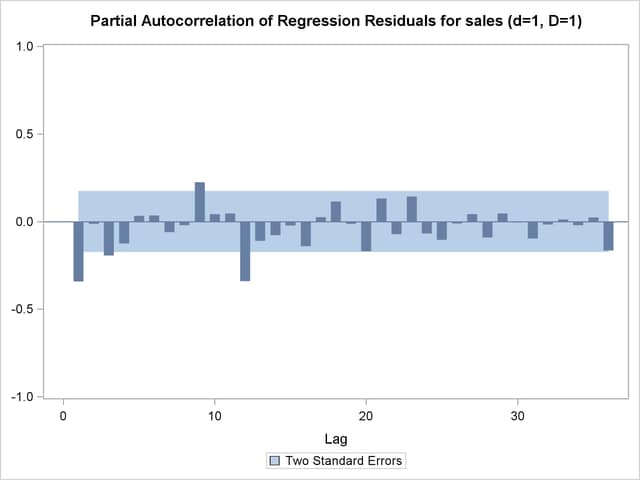
| Partial Autocorrelations of Regression Residuals for ARIMA Model Identification |
||
|---|---|---|
| For Variable sales | ||
| Differencing: Nonseasonal Order=1 Seasonal Order=1 |
||
| Lag | Correlation | Standard Error |
| 1 | -0.34112 | 0.08737 |
| 2 | -0.01281 | 0.08737 |
| 3 | -0.19266 | 0.08737 |
| 4 | -0.12503 | 0.08737 |
| 5 | 0.03309 | 0.08737 |
| 6 | 0.03468 | 0.08737 |
| 7 | -0.06019 | 0.08737 |
| 8 | -0.02022 | 0.08737 |
| 9 | 0.22558 | 0.08737 |
| 10 | 0.04307 | 0.08737 |
| 11 | 0.04659 | 0.08737 |
| 12 | -0.33869 | 0.08737 |
| 13 | -0.10918 | 0.08737 |
| 14 | -0.07684 | 0.08737 |
| 15 | -0.02175 | 0.08737 |
| 16 | -0.13955 | 0.08737 |
| 17 | 0.02589 | 0.08737 |
| 18 | 0.11482 | 0.08737 |
| 19 | -0.01316 | 0.08737 |
| 20 | -0.16743 | 0.08737 |
| 21 | 0.13240 | 0.08737 |
| 22 | -0.07204 | 0.08737 |
| 23 | 0.14285 | 0.08737 |
| 24 | -0.06733 | 0.08737 |
| 25 | -0.10267 | 0.08737 |
| 26 | -0.01007 | 0.08737 |
| 27 | 0.04378 | 0.08737 |
| 28 | -0.08995 | 0.08737 |
| 29 | 0.04690 | 0.08737 |
| 30 | -0.00490 | 0.08737 |
| 31 | -0.09638 | 0.08737 |
| 32 | -0.01528 | 0.08737 |
| 33 | 0.01150 | 0.08737 |
| 34 | -0.01916 | 0.08737 |
| 35 | 0.02303 | 0.08737 |
| 36 | -0.16488 | 0.08737 |
Copyright © SAS Institute, Inc. All Rights Reserved.