| The X12 Procedure |
| X11 Statement |
The X11 statement is an optional statement for invoking seasonal adjustment by an enhanced version of the methodology of the Census Bureau X-11 and X-11Q programs. You can control the type of seasonal adjustment decomposition calculated with the MODE= option. The output includes the final tables and diagnostics for the X-11 seasonal adjustment method listed in Table 34.5. Tables E1, E2, E3, C20, D1, and D7 are not displayed by default; however, you can display these tables by requesting them in the TABLES statement.
Table Name |
Description |
B1 |
Original series, adjusted for prior effects and forecast extended |
C17 |
Final weights for the irregular component |
C20 |
Final extreme value adjustment factors |
D1 |
Modified original data, D iteration |
D7 |
Preliminary trend cycle, D iteration |
D8 |
Final unmodified SI ratios (differences) |
D8A |
F tests for stable and moving seasonality, D8 |
D9 |
Final replacement values for extreme SI ratios (differences), D iteration |
D9A |
Moving seasonality ratios for each period |
SeasonalFilter |
Seasonal filter statistics for table D10 |
D10 |
Final seasonal factors |
D10B |
Seasonal factors, adjusted for user-defined seasonal |
D10D |
Final seasonal difference |
D11 |
Final seasonally adjusted series |
D11A |
Final seasonally adjusted series with forced yearly totals |
D11R |
Rounded final seasonally adjusted series (with forced yearly totals) |
TrendFilter |
Trend filter statistics for table D12 |
D12 |
Final trend cycle |
D13 |
Final irregular component |
D16 |
Combined seasonal and trading day factors |
D16B |
Final adjustment differences |
D18 |
Combined calendar adjustment factors |
E1 |
Original data modified for extremes |
E2 |
Modified seasonally adjusted series |
E3 |
Modified irregular series |
E4 |
Ratio of yearly totals of original and seasonally adjusted series |
E5 |
Percent changes (differences) in original series |
E6 |
Percent changes (differences) in seasonally adjusted series |
E6A |
Percent changes (differences) in seasonally adjusted series with forced yearly totals (D11.A) |
E6R |
Percent changes (differences) in rounded seasonally adjusted series (D11.R) |
E7 |
Percent changes (differences) in final trend component series |
E8 |
Percent changes (differences) in original series adjusted for calendar factors (A18) |
F2A–F2I |
X11 diagnostic summary |
F3 |
Monitoring and quality assessment statistics |
F4 |
Day of the week trading day component factors |
G |
Spectral plots |
For more details about the X-11 seasonal adjustment diagnostics, see Shiskin, Young, and Musgrave (1967), Lothian and Morry (1978a), and Ladiray and Quenneville (2001).
The following options can appear in the X11 statement:
- MODE=ADD
- MODE=MULT
- MODE=LOGADD
- MODE=PSEUDOADD
determines the mode of the seasonal adjustment decomposition to be performed. The four option choices correspond to additive, multiplicative, log-additive, and pseudo-additive decomposition, respectively. If this option is omitted, the procedure performs multiplicative adjustments. Table 34.6 shows the values of the MODE= option and the corresponding models for the original (O) and the seasonally adjusted (SA) series.
Table 34.6 Modes of Seasonal Adjustment and Their Models Value of Mode Option
Name
Model for

Model for
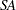
MULT
Multiplicative
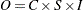
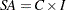
ADD
Additive
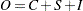
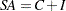
PSEUDOADD
Pseudo-additive
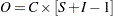
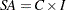
LOGADD
Log-additive
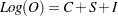
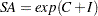
- OUTFCST
- OUTFORECAST
determines whether forecasts are included in certain tables sent to the output data set. If OUTFORECAST is specified, then forecast values are included in the output data set for tables A6, A7, A8, A9, A10, B1, D10, D10B, D10D, D16, D16B, and D18. The default is not to include forecasts.
- SEASONALMA=S3X1
- SEASONALMA=S3X3
- SEASONALMA=S3X5
- SEASONALMA=S3X9
- SEASONALMA=S3X15
- SEASONALMA=STABLE
- SEASONALMA=X11DEFAULT
- SEASONALMA=MSR
specifies which seasonal moving average (also called seasonal "filter") is used to estimate the seasonal factors. These seasonal moving averages are
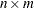 moving averages, meaning that an
moving averages, meaning that an  -term simple average is taken of a sequence of consecutive
-term simple average is taken of a sequence of consecutive  -term simple averages. X11DEFAULT is the method used by the U.S. Census Bureau’s X-11-ARIMA program. The default for PROC X12 is SEASONALMA=MSR, which is the methodology of Statistic Canada’s X-11-ARIMA/88 program.
-term simple averages. X11DEFAULT is the method used by the U.S. Census Bureau’s X-11-ARIMA program. The default for PROC X12 is SEASONALMA=MSR, which is the methodology of Statistic Canada’s X-11-ARIMA/88 program.
Table 34.7 describes the seasonal filter options available for the entire series:Table 34.7 X-12-ARIMA Seasonal Filter Options and Descriptions Filter Name
Description of Filter
S3X1
A
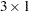 moving average
moving average S3X3
A
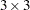 moving average
moving average S3X5
A
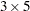 moving average
moving average S3X9
A
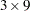 moving average
moving average S3X15
A
 moving average
moving average STABLE
Stable seasonal filter. A single seasonal factor for each
calendar month or quarter is generated by calculating the simple
average of all the values for each month or quarter (taken after
detrending and outlier adjustment).
X11DEFAULT
A
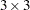 moving average is used to calculate the
moving average is used to calculate the initial seasonal factors in each iteration, and a
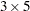 moving
moving average to calculate the final seasonal factors
MSR
Filter chosen automatically by using the moving seasonality
ratio of X-11-ARIMA/88 (Dagum; 1988)
- SIGMALIM=(lower limit, upper limit )
- SIGMALIM=(lower limit )
- SIGMALIM=( , upper limit )
specifies the lower and upper sigma limits in standard deviation units which are used to identify and down-weight extreme irregular values in the internal seasonal adjustment computations. One or both limits can be specified. The lower limit must be greater than
 and not greater than the upper limit. If the lower sigma limit is not specified, then it defaults to a value of
and not greater than the upper limit. If the lower sigma limit is not specified, then it defaults to a value of 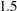 . The default upper sigma limit is
. The default upper sigma limit is 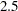 . The comma must be used if the upper limit is specified.
. The comma must be used if the upper limit is specified. Table 34.8 shows the effect of the SIGMALIM= option on the weights that are applied to the internal irregular values.
Table 34.8 Weights for Irregular Values Weight
Sigma Limit

If
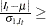 upper limit
upper limit Partial weight
If lower limit
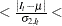 upper limit
upper limit 
If
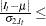 lower limit
lower limit In Table 34.8,
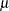 is the theoretical mean of the irregular component, and
is the theoretical mean of the irregular component, and  and
and 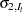 are the respective estimates of the standard deviation of the irregular component before and after extreme values are removed. The estimates of the standard deviation
are the respective estimates of the standard deviation of the irregular component before and after extreme values are removed. The estimates of the standard deviation  and
and 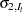 vary with respect to
vary with respect to  , and they are the same if no extreme values are removed. If they are different (
, and they are the same if no extreme values are removed. If they are different (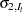 <
<  ), then the first line in Table 34.8 is reevaluated with
), then the first line in Table 34.8 is reevaluated with 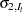 . In the special case where the lower limit equals the upper limit, the weight is
. In the special case where the lower limit equals the upper limit, the weight is  for
for 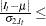 lower limit, and
lower limit, and  otherwise. For more information about how extreme irregular values are handled in the X11 computations, see Ladiray and Quenneville; 2001, pp. 53–68, 122–125.
otherwise. For more information about how extreme irregular values are handled in the X11 computations, see Ladiray and Quenneville; 2001, pp. 53–68, 122–125. - TRENDMA=value
specifies which Henderson moving average is used to estimate the final trend cycle. Any odd number greater than one and less than or equal to 101 can be specified, for example, TRENDMA=23. If the TRENDMA= option is not specified, the program selects a trend moving average based on statistical characteristics of the data. For monthly series, a 9-, 13-, or 23-term Henderson moving average is selected. For quarterly series, the program chooses either a 5- or a 7-term Henderson moving average.
- TYPE=SA
- TYPE=SUMMARY
- TYPE=TREND
specifies the method used to calculate the final seasonally adjusted series (Table D11). The default method is TYPE=SA. This method assumes that the original series has not been seasonally adjusted. For method TYPE=SUMMARY, the trend cycle, irregular, trading day, and holiday factors are calculated, but not removed from the seasonally adjusted series. Thus, for TYPE=SUMMARY, Table D11 is the same as the original series. For TYPE=TREND, trading day, holiday, and prior adjustment factors are removed from the original series to calculate the seasonally adjusted series (Table D11) and also are used in the calculation of the final trend (Table D12).
- FINAL=AO
- FINAL=LS
- FINAL=TC
- FINAL=ALL
- FINAL=(options)
lists the types of prior adjustment factors, obtained from the EVENT, REGRESSION and OUTLIER statements, that are to be removed from the final seasonally adjusted series. Additive outliers are removed by specifying FINAL=AO. Level change and ramp outliers are removed by specifying FINAL=LS. Temporary change outliers are removed by specifying FINAL=TC. All the preceding are removed by specifying FINAL=ALL or by specifying all the options in parentheses, FINAL=(AO LS TC). If this option is not specified, the final seasonally adjusted series contains these effects.
- FORCE=TOTALS
- FORCE=ROUND
- FORCE=BOTH
specifies that the seasonally adjusted series be modified to: (a) force the yearly totals of the seasonally adjusted series and the original series to be the same (FORCE=TOTALS), (b) adjust the seasonally adjusted values for each calendar year so that the sum of the rounded seasonally adjusted series for any year equals the rounded annual total (FORCE=ROUND), or (c) first force the yearly totals, then round the adjusted series (FORCE=BOTH). When FORCE=TOTALS is specified, the differences between the annual totals is distributed over the seasonally adjusted values in a way that approximately preserves the month-to-month (or quarter-to-quarter) movements of the original series. For more details, see Huot (1975) and Cholette (1979). This forcing procedure is not recommended if the seasonal pattern is changing or if trading day adjustment is performed. Forcing the seasonally adjusted totals to be the same as the original series annual totals can degrade the quality of the seasonal adjustment, especially when the seasonal pattern is undergoing change. It is not natural if trading day adjustment is performed because the aggregate trading day effect over a year is variable and moderately different from zero.
Copyright © SAS Institute, Inc. All Rights Reserved.