Example 31.5 Trend Removal Using the Hodrick-Prescott Filter

Hodrick-Prescott filter (see Hodrick and Prescott (1997)) is a popular tool in macroeconomics for fitting smooth trend to time series. It is well known that the trend computation according to this filter is equivalent to fitting the local linear trend plus irregular model with the level disturbance variance restricted to zero and the slope disturbance variance restricted to be a suitable multiple of the irregular component variance. The multiple used depends on the frequency of the series; for example, for quarterly series the commonly recommended multiple is . For other intervals there is no consensus, but a frequently suggested value for monthly series is and the value for an annual series can range from 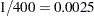to . The data set considered in this example consists of quarterly GNP values for the United States from 1960 to 1991. 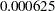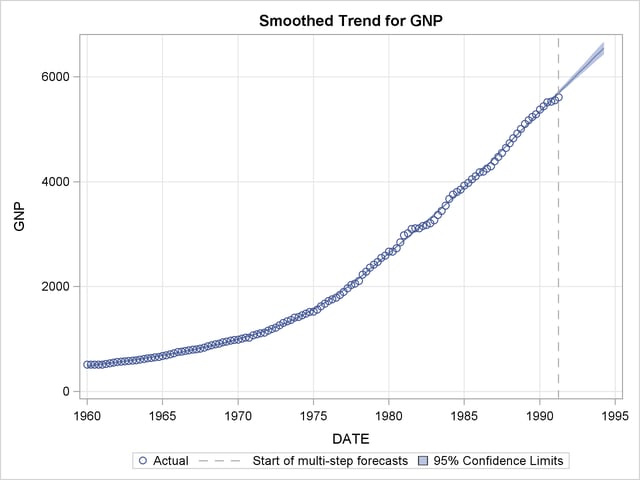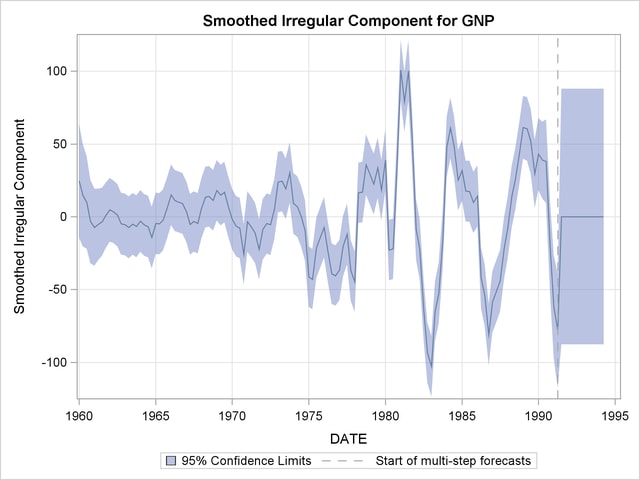In the UCM procedure statements that follow, the presence of the PROFILE option in the ESTIMATE statement implies that the restriction that the disturbance variance of the slope component be fixed at is interpreted differently: it implies that the disturbance variance of the slope component be restricted to be 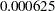times the estimated irregular component variance, as needed for the Hodrick-Prescott filter. The plot of the fitted trend is shown in Output 31.5.1, and the plot of the smoothed irregular component, which corresponds to the detrended series, is given in Output 31.5.2. The detrended series can be further analyzed for business cycles.

ods graphics on;
proc ucm data=sashelp.gnp;
   id date interval=qtr;
   model gnp;
   irregular plot=smooth;
   level var=0 noest plot=smooth;
   slope var=0.000625 noest;
   estimate PROFILE;
   forecast plot=(decomp);
run;

Output 31.5.1 Smoothed Trend for the GNP Series as per the Hodrick-Prescott Filter

Output 31.5.2 Detrended GNP Series