| The TIMESERIES Procedure |
| Singular Spectrum Analysis |
Given a time series, 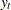 , for
, for  , and a window length,
, and a window length,  , singular spectrum analysis Golyandina, Nekrutkin, and Zhigljavsky (2001) decompose the time series into spectral groupings using the following steps:
, singular spectrum analysis Golyandina, Nekrutkin, and Zhigljavsky (2001) decompose the time series into spectral groupings using the following steps:
Embedding Step
Using the time series, form a  trajectory matrix,
trajectory matrix,  , with elements
, with elements
 |
such that  for
for 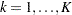 and
and 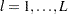 and where
and where  . By definition
. By definition 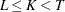 , because
, because 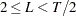 .
.
Decomposition Step
Using the trajectory matrix,  , apply singular value decomposition to the trajectory matrix
, apply singular value decomposition to the trajectory matrix
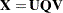 |
where  represents the
represents the  matrix that contains the left-hand-side (LHS) eigenvectors, where
matrix that contains the left-hand-side (LHS) eigenvectors, where  represents the diagonal
represents the diagonal 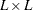 matrix that contains the singular values, and where
matrix that contains the singular values, and where  represents the
represents the 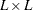 matrix that conatins the right-hand-side (RHS) eigenvectors.
matrix that conatins the right-hand-side (RHS) eigenvectors.
Therefore,
 |
where 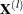 represents the
represents the  principal component matrix,
principal component matrix, 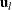 represents the
represents the 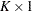 left-hand-side (LHS) eigenvector,
left-hand-side (LHS) eigenvector,  represents the singular value, and
represents the singular value, and 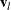 represents the
represents the  right-hand-side (RHS) eigenvector associated with the
right-hand-side (RHS) eigenvector associated with the 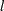 th window index.
th window index.
Grouping Step
For each group index,  , define a group of window indices
, define a group of window indices 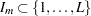 . Let
. Let
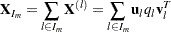 |
represent the grouped trajectory matrix for group 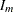 . If groupings represent a spectral partition,
. If groupings represent a spectral partition,
 |
then according to the singular value decomposition theory,
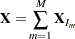 |
Averaging Step
For each group index,  , compute the diagonal average of
, compute the diagonal average of  ,
,
 |
where
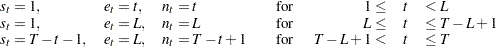 |
If the groupings represent a spectral partition, then by definition
 |
Hence, singular spectrum analysis additively decomposes the original time series, 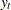 , into
, into  component series
component series 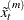 for
for  .
.
Specifying the Window Length
You can explicitly specify the maximum window length, 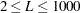 , using the LENGTH= option or implicitly specify the window length using the INTERVAL= option in the ID statement or the SEASONALITY= option in the PROC TIMESERIES statement.
, using the LENGTH= option or implicitly specify the window length using the INTERVAL= option in the ID statement or the SEASONALITY= option in the PROC TIMESERIES statement.
Either way the window length is reduced based on the accumulated time series length,  , to enforce the requirement that
, to enforce the requirement that 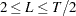 .
.
Specifying the Groups
You can use the GROUPS= option to explicitly specify the composition and number of groups,  or use the THRESHOLDPCT= option in the SSA statement to implicitly specify the grouping. The THRESHOLDPCT= option is useful for removing noise or less dominant patterns from the accumulated time series.
or use the THRESHOLDPCT= option in the SSA statement to implicitly specify the grouping. The THRESHOLDPCT= option is useful for removing noise or less dominant patterns from the accumulated time series.
Let 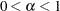 be the cumulative percent singular value THRESHOLDPCT=. Then the last group,
be the cumulative percent singular value THRESHOLDPCT=. Then the last group, 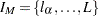 , is determined by the smallest value such that
, is determined by the smallest value such that
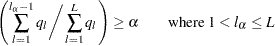 |
Using this rule, the last group,  , describes the least dominant patterns in the time series and the size of the last group is at least one and is less than the window length,
, describes the least dominant patterns in the time series and the size of the last group is at least one and is less than the window length, 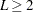 .
.
Copyright © SAS Institute, Inc. All Rights Reserved.