| The TIMESERIES Procedure |
| Spectral Density Analysis |
Spectral analysis can be performed on the working series by specifying the OUTSPECTRA= option or by specifying the PLOTS=PERIODOGRAM or PLOTS=SPECTRUM option in the PROC TIMESERIES statement. PROC TIMESERIES uses the finite Fourier transform to decompose data series into a sum of sine and cosine terms of different amplitudes and wavelengths. The Fourier transform decomposition of the series 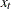 is
is
 |
where

is the time subscript,
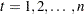

are the equally spaced time series data

is the number of observations in the time series

is the number of frequencies in the Fourier decomposition:
 if
if  is even,
is even,  if
if  is odd
is odd 
is the mean term:


are the cosine coefficients

are the sine coefficients

are the Fourier frequencies:

Functions of the Fourier coefficients  and
and  can be plotted against frequency or against wave length to form periodograms. The amplitude periodogram
can be plotted against frequency or against wave length to form periodograms. The amplitude periodogram  is defined as follows:
is defined as follows:
 |
The Fourier decomposition is performed after the ACCUMULATE=, DIF=, SDIF= and TRANSFORM= options in the ID and VAR statements have been applied.
Computational Method
If the number of observations,  , factors into prime integers that are less than or equal to 23, and the product of the square-free factors of
, factors into prime integers that are less than or equal to 23, and the product of the square-free factors of  is less than 210, then the procedure uses the fast Fourier transform developed by Cooley and Tukey (1965) and implemented by Singleton (1969). If
is less than 210, then the procedure uses the fast Fourier transform developed by Cooley and Tukey (1965) and implemented by Singleton (1969). If  cannot be factored in this way, then the procedure uses a Chirp-Z algorithm similar to that proposed by Monro and Branch (1976).
cannot be factored in this way, then the procedure uses a Chirp-Z algorithm similar to that proposed by Monro and Branch (1976).
Missing Values
Missing values are replaced with an estimate of the mean to perform spectral analyses. This treatment of a series with missing values is consistent with the approach used by Priestley (1981).
Using Specification of Weight Constants
Any number of weighting constants can be specified. The constants are interpreted symmetrically about the middle weight. The middle constant (or the constant to the right of the middle if an even number of weight constants is specified) is the relative weight of the current periodogram ordinate. The constant immediately following the middle one is the relative weight of the next periodogram ordinate, and so on. The actual weights used in the smoothing process are the weights specified in the WEIGHTS option, scaled so that they sum to 1.
The moving average calculation reflects at each end of the periodogram to accommodate the periodicity of the periodogram function.
For example, a simple triangular weighting can be specified using the following WEIGHTS option:
spectra / weights 1 2 3 2 1;
Using Kernel Specifications
You can specify one of ten different kernels in the SPECTRA statement. The two parameters  and
and 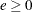 are used to compute the bandwidth parameter
are used to compute the bandwidth parameter
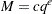 |
where  is the number of periodogram ordinates + 1,
is the number of periodogram ordinates + 1,
 |
To specify the bandwidth explicitly, set 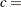 to the desired bandwidth and
to the desired bandwidth and  .
.
For example, a Parzen kernel with a support of 11 periodogram ordinates can be specified using the following kernel option:
spectra / parzen c=5 expon=0;
Kernels are used to smooth the periodogram by using a weighted moving average of nearby points. A smoothed periodogram is defined by the equation
 |
where  is the kernel or weight function.
is the kernel or weight function.
At the endpoints, the moving average is computed cyclically; that is,
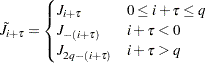 |
where 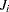 is the
is the  periodogram ordinate.
periodogram ordinate.
The TIMESERIES procedure supports the following kernels:
BART: Bartlett kernel
 |
 |
 |
PARZEN: Parzen kernel
 |
 |
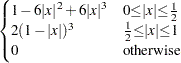 |
QS: quadratic spectral kernel
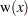 |
 |
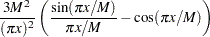 |
TUKEY: Tukey-Hanning kernel
 |
 |
 |
TRUNCAT: truncated kernel
 |
 |
 |
Alternatively, kernel functions can be applied as filters that estimate the autocovariance function in the time domain prior to computing the periodogram by using the DOMAIN=TIME option as
 |
where  . To approximate this operation, complementary kernel weighting functions,
. To approximate this operation, complementary kernel weighting functions, 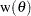 , can be used to smooth the periodogram by using the same cyclical moving average computation described previously. The frequencies used to weight periodogram ordinates are
, can be used to smooth the periodogram by using the same cyclical moving average computation described previously. The frequencies used to weight periodogram ordinates are  . The five complementary weighting functions available to smooth the periodogram in this manner are:
. The five complementary weighting functions available to smooth the periodogram in this manner are:
BART: Bartlett equivalent lag window filter
 |
 |
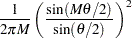 |
PARZEN: Parzen equivalent lag window filter
 |
 |
 |
QS: quadratic spectral equivalent lag window filter
 |
 |
 |
TUKEY: Tukey-Hanning equivalent lag window filter
 |
 |
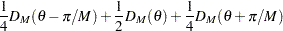 |
|||
 |
 |
 |
TRUNC: truncated equivalent lag window filter
 |
 |
 |
Copyright © SAS Institute, Inc. All Rights Reserved.