PROC QLIM: Sample Selection Model with Truncation and Censoring

The QLIM Procedure

Example 21.5 Sample Selection Model with Truncation and Censoring

In this example the data are generated such that the selection variable is discrete and the variable Y is truncated from below by zero. The program follows, with the results shown in Output 21.5.1:

data trunc;
   keep z y x1 x2;
   do i = 1 to 500;
      x1 = rannor( 19283 );
      x2 = rannor( 19283 );
      u1 = rannor( 19283 );
      u2 = rannor( 19283 );
      zl = 1 + 2 * x1 + 3 * x2 + u1;
      y = 3 + 4 * x1 - 2 * x2 + u1*.2 + u2;
      if ( zl > 0 ) then z = 1;
      else z = 0;
      if y>=0 then output;
   end;
run;

 /*-- Sample Selection with Truncation --*/
 proc qlim data=trunc method=qn;
    model z = x1 x2 / discrete;
    model y = x1 x2 / select(z=1) truncated(lb=0);
 run;

Output 21.5.1 Sample Selection with Truncation

Binary Data

The QLIM Procedure

Model Fit Summary
Number of Endogenous Variables	2
Endogenous Variable	z y
Number of Observations	379
Log Likelihood	-344.10722
Maximum Absolute Gradient	4.95535E-6
Number of Iterations	17
Optimization Method	Quasi-Newton
AIC	704.21444
Schwarz Criterion	735.71473

Parameter Estimates
Parameter	DF	Estimate	Standard Error	t Value	Approx Pr > \|t\|
y.Intercept	1	3.014158	0.128548	23.45	<.0001
y.x1	1	3.995671	0.099599	40.12	<.0001
y.x2	1	-1.972697	0.096385	-20.47	<.0001
_Sigma.y	1	0.923428	0.047233	19.55	<.0001
z.Intercept	1	0.949444	0.190265	4.99	<.0001
z.x1	1	2.163928	0.288384	7.50	<.0001
z.x2	1	3.134213	0.379251	8.26	<.0001
_Rho	1	0.494356	0.176542	2.80	0.0051

In the following statements the data are generated such that the selection variable is discrete and the variable 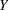$\text{[math]}$ is censored from below by zero. The results are shown in Output 21.5.2.

data cens;
   keep z y x1 x2;
   do i = 1 to 500;
      x1 = rannor( 19283 );
      x2 = rannor( 19283 );
      u1 = rannor( 19283 );
      u2 = rannor( 19283 );
      zl = 1 + 2 * x1 + 3 * x2 + u1;
      yl = 3 + 4 * x1 - 2 * x2 + u1*.2 + u2;
      if ( zl > 0 ) then z = 1;
      else               z = 0;
      if ( yl > 0 ) then y = yl;
      else               y = 0;
      output;
   end;
run;

 /*-- Sample Selection with Censoring --*/
 proc qlim data=cens method=qn;
    model z = x1 x2 / discrete;
    model y = x1 x2 / select(z=1) censored(lb=0);
 run;

Output 21.5.2 Sample Selection with Censoring

Binary Data

The QLIM Procedure

Model Fit Summary
Number of Endogenous Variables	2
Endogenous Variable	z y
Number of Observations	500
Log Likelihood	-399.78508
Maximum Absolute Gradient	2.30443E-6
Number of Iterations	19
Optimization Method	Quasi-Newton
AIC	815.57015
Schwarz Criterion	849.28702

Parameter Estimates
Parameter	DF	Estimate	Standard Error	t Value	Approx Pr > \|t\|
y.Intercept	1	3.074276	0.111617	27.54	<.0001
y.x1	1	3.963619	0.085796	46.20	<.0001
y.x2	1	-2.023548	0.088714	-22.81	<.0001
_Sigma.y	1	0.920860	0.043278	21.28	<.0001
z.Intercept	1	1.013610	0.154081	6.58	<.0001
z.x1	1	2.256922	0.255999	8.82	<.0001
z.x2	1	3.302692	0.342168	9.65	<.0001
_Rho	1	0.350776	0.197093	1.78	0.0751

Top of Page