| The X12 Procedure |
Example 32.4 RegARIMA Automatic Model Selection
This example demonstrates two of the new features available through the X-12-ARIMA method that are not available by using the previous X-11 and X-11-ARIMA methods: regARIMA modeling and TRAMO-based automatic model selection. Assume that the same data set is used as in the previous examples.
title 'TRAMO Automatic Model Identification';
ods select ModelEstimation.AutoModel.UnitRootTestModel
ModelEstimation.AutoModel.UnitRootTest
ModelEstimation.AutoModel.AutoChoiceModel
ModelEstimation.AutoModel.Best5Model
ModelEstimation.AutoModel.AutomaticModelChoice
ModelEstimation.AutoModel.FinalModelChoice
ModelEstimation.AutoModel.AutomdlNote;
proc x12 data=sales date=date;
var sales;
transform function=log;
regression predefined=td;
automdl maxorder=(1,1)
print=unitroottest unitroottestmdl autochoicemdl best5model;
estimate;
x11;
output out=out(obs=23) a1 a2 a6 b1 c17 c20 d1 d7 d8 d9 d10
d11 d12 d13 d16 d18;
run;
proc print data=out(obs=23);
title 'Output Variables Related to Trading Day Regression';
run;
The automatic model selection output is shown in Output 32.4.1, Output 32.4.2, and Output 32.4.3. The first table, "ARIMA Estimate for Unit Root Identification," gives details of the method that TRAMO uses to automatically select the orders of differencing. The second table, "Results of Unit Root Test for Identifying Orders of Differencing," shows that a regular difference order of 1 and a seasonal difference order of 1 has been determined by TRAMO. The third table, "Models estimated by Automatic ARIMA Model Selection procedure," shows all the models examined by the TRAMO-based method. The fourth table, "Best Five ARIMA Models Chosen by Automatic Modeling," shows the top five models in order of rank and their BIC2 statistic. The fifth table, "Comparison of Automatically Selected Model and Default Model," compares the model selected by the TRAMO model to the default X-12-ARIMA model. The sixth table, "Final Automatic Model Selection," shows which model was actually selected.
| ARIMA Estimates for Unit Root Identification | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| For variable sales | |||||||||||||||
| Model Number | Estimation Method | ARMA | |||||||||||||
| Estimated Model | Parameter | Estimate | |||||||||||||
| 1 | H-R | ( 2, | 0, | 0) | ( 1, | 0, | 0) | NS_AR_1 | 0.67540 | ||||||
| H-R | ( 2, | 0, | 0) | ( 1, | 0, | 0) | NS_AR_2 | 0.28425 | |||||||
| H-R | ( 2, | 0, | 0) | ( 1, | 0, | 0) | S_AR_12 | 0.91963 | |||||||
| 2 | H-R | ( 1, | 1, | 1) | ( 1, | 0, | 1) | NS_AR_1 | 0.13418 | ||||||
| H-R | ( 1, | 1, | 1) | ( 1, | 0, | 1) | S_AR_12 | 0.98500 | |||||||
| H-R | ( 1, | 1, | 1) | ( 1, | 0, | 1) | NS_MA_1 | 0.47884 | |||||||
| H-R | ( 1, | 1, | 1) | ( 1, | 0, | 1) | S_MA_12 | 0.51726 | |||||||
| 3 | H-R | ( 1, | 1, | 1) | ( 1, | 1, | 1) | NS_AR_1 | -0.39269 | ||||||
| H-R | ( 1, | 1, | 1) | ( 1, | 1, | 1) | S_AR_12 | 0.06223 | |||||||
| H-R | ( 1, | 1, | 1) | ( 1, | 1, | 1) | NS_MA_1 | -0.09570 | |||||||
| H-R | ( 1, | 1, | 1) | ( 1, | 1, | 1) | S_MA_12 | 0.58536 | |||||||
| Models estimated by Automatic ARIMA Model Selection procedure | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| For variable sales | ||||||||||||||||
| Model Number | ARMA | Statistics of Fit | ||||||||||||||
| Estimated Model | Parameter | Estimate | BIC | BIC2 | ||||||||||||
| 1 | ( 3, | 1, | 0) | ( 0, | 1, | 0) | NS_AR_1 | -0.33524 | ||||||||
| ( 3, | 1, | 0) | ( 0, | 1, | 0) | NS_AR_2 | -0.05558 | |||||||||
| ( 3, | 1, | 0) | ( 0, | 1, | 0) | NS_AR_3 | -0.15649 | |||||||||
| ( 3, | 1, | 0) | ( 0, | 1, | 0) | 1024.469 | -3.40549 | |||||||||
| 2 | ( 3, | 1, | 0) | ( 0, | 1, | 1) | NS_AR_1 | -0.33186 | ||||||||
| ( 3, | 1, | 0) | ( 0, | 1, | 1) | NS_AR_2 | -0.05823 | |||||||||
| ( 3, | 1, | 0) | ( 0, | 1, | 1) | NS_AR_3 | -0.15200 | |||||||||
| ( 3, | 1, | 0) | ( 0, | 1, | 1) | S_MA_12 | 0.55279 | |||||||||
| ( 3, | 1, | 0) | ( 0, | 1, | 1) | 993.7880 | -3.63970 | |||||||||
| 3 | ( 3, | 1, | 0) | ( 1, | 1, | 0) | NS_AR_1 | -0.38673 | ||||||||
| ( 3, | 1, | 0) | ( 1, | 1, | 0) | NS_AR_2 | -0.08768 | |||||||||
| ( 3, | 1, | 0) | ( 1, | 1, | 0) | NS_AR_3 | -0.18143 | |||||||||
| ( 3, | 1, | 0) | ( 1, | 1, | 0) | S_AR_12 | -0.47336 | |||||||||
| ( 3, | 1, | 0) | ( 1, | 1, | 0) | 1000.224 | -3.59057 | |||||||||
| 4 | ( 3, | 1, | 0) | ( 1, | 1, | 1) | NS_AR_1 | -0.34352 | ||||||||
| ( 3, | 1, | 0) | ( 1, | 1, | 1) | NS_AR_2 | -0.06504 | |||||||||
| ( 3, | 1, | 0) | ( 1, | 1, | 1) | NS_AR_3 | -0.15728 | |||||||||
| ( 3, | 1, | 0) | ( 1, | 1, | 1) | S_AR_12 | -0.12163 | |||||||||
| ( 3, | 1, | 0) | ( 1, | 1, | 1) | S_MA_12 | 0.47073 | |||||||||
| ( 3, | 1, | 0) | ( 1, | 1, | 1) | 998.0548 | -3.60713 | |||||||||
| 5 | ( 0, | 1, | 0) | ( 0, | 1, | 1) | S_MA_12 | 0.60446 | ||||||||
| ( 0, | 1, | 0) | ( 0, | 1, | 1) | 996.8560 | -3.61628 | |||||||||
| 6 | ( 0, | 1, | 1) | ( 0, | 1, | 1) | NS_MA_1 | 0.36272 | ||||||||
| ( 0, | 1, | 1) | ( 0, | 1, | 1) | S_MA_12 | 0.55599 | |||||||||
| ( 0, | 1, | 1) | ( 0, | 1, | 1) | 986.6405 | -3.69426 | |||||||||
| 7 | ( 1, | 1, | 0) | ( 0, | 1, | 1) | NS_AR_1 | -0.32734 | ||||||||
| ( 1, | 1, | 0) | ( 0, | 1, | 1) | S_MA_12 | 0.55834 | |||||||||
| ( 1, | 1, | 0) | ( 0, | 1, | 1) | 987.1500 | -3.69037 | |||||||||
| 8 | ( 1, | 1, | 1) | ( 0, | 1, | 1) | NS_AR_1 | 0.17833 | ||||||||
| ( 1, | 1, | 1) | ( 0, | 1, | 1) | NS_MA_1 | 0.52867 | |||||||||
| ( 1, | 1, | 1) | ( 0, | 1, | 1) | S_MA_12 | 0.56212 | |||||||||
| ( 1, | 1, | 1) | ( 0, | 1, | 1) | 991.2363 | -3.65918 | |||||||||
| 9 | ( 0, | 1, | 1) | ( 0, | 1, | 0) | NS_MA_1 | 0.36005 | ||||||||
| ( 0, | 1, | 1) | ( 0, | 1, | 0) | 1017.770 | -3.45663 | |||||||||
Methodology based on research by Gomez and Maravall (2000).
| Best Five ARIMA Models Chosen by Automatic Modeling |
|||||||||
|---|---|---|---|---|---|---|---|---|---|
| For variable sales | |||||||||
| Rank | Estimated Model | BIC2 | |||||||
| 1 | ( 0, | 1, | 1) | ( 0, | 1, | 1) | -3.69426 | ||
| 2 | ( 1, | 1, | 0) | ( 0, | 1, | 1) | -3.69037 | ||
| 3 | ( 1, | 1, | 1) | ( 0, | 1, | 1) | -3.65918 | ||
| 4 | ( 0, | 1, | 0) | ( 0, | 1, | 1) | -3.61628 | ||
| 5 | ( 0, | 1, | 1) | ( 0, | 1, | 0) | -3.45663 | ||
| Comparison of Automatically Selected Model and Default Model | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| For variable sales | |||||||||||||
| Source of Candidate Models | Statistics of Fit | ||||||||||||
| Estimated Model | Plbox | Rvr | Number of Outliers |
||||||||||
| Automatic Model Choice | ( 0, | 1, | 1) | ( 0, | 1, | 1) | 0.62560 | 0.03546 | 0 | ||||
| Airline Model (Default) | ( 0, | 1, | 1) | ( 0, | 1, | 1) | 0.62561 | 0.03546 | 0 | ||||
| Final Automatic Model Selection | ||||||
|---|---|---|---|---|---|---|
| For variable sales | ||||||
| Source of Model | Estimated Model | |||||
| Automatic Model Choice | ( 0, | 1, | 1) | ( 0, | 1, | 1) |
Table 32.10 and Output 32.4.4 illustrate the regARIMA modeling method. Table 32.10 shows the relationship between the output variables in PROC X12 that results from a regARIMA model. Note that some of these formulas apply only to this example. Output 32.4.4 shows the values of these variables for the first 23 observations in the example.
Table |
Title |
Type |
Formula |
|---|---|---|---|
A1 |
time series data (for the span analyzed) |
data |
input |
A2 |
prior-adjustment factors |
factor |
calculated from regression |
leap year (from trading day regression) |
|||
adjustments |
|||
A6 |
regARIMA trading day component |
factor |
calculated from regression |
leap year prior adjustments included |
|||
from Table A2 |
|||
B1 |
original series (prior adjusted) |
data |
|
(adjusted for regARIMA factors) |
* because only TD specified |
||
C17 |
final weights for irregular component |
factor |
calculated using moving |
standard deviation |
|||
C20 |
final extreme value adjustment factors |
factor |
calculated using C16 and C17 |
D1 |
modified original data, D iteration |
data |
|
|
|||
** C19=B1 in this example |
|||
D7 |
preliminary trend cycle, D iteration |
data |
calculated using Henderson |
moving average |
|||
D8 |
final unmodified SI ratios |
factor |
|
|
|||
*** TD specified in regression |
|||
D9 |
final replacement values for SI ratios |
factor |
if C17 shows extreme values, |
|
|||
|
|||
D10 |
final seasonal factors |
factor |
calculated using moving averages |
D11 |
final seasonally adjusted data |
data |
|
(also adjusted for trading day) |
|
||
**** |
|||
D12 |
final trend cycle |
data |
calculated using Henderson |
moving average |
|||
D13 |
final irregular component |
factor |
|
D16 |
combined adjustment factors |
factor |
|
(includes seasonal, trading day factors) |
|||
D18 |
combined calendar adjustment factors |
factor |
|
(includes trading day factors) |
|
||
***** regression TD is the only |
|||
calendar adjustment factor |
|||
in this example |
| Output Variables Related to Trading Day Regression |
| Obs | DATE | sales_A1 | sales_A2 | sales_A6 | sales_B1 | sales_C17 | sales_C20 | sales_D1 | sales_D7 | sales_D8 | sales_D9 | sales_D10 | sales_D11 | sales_D12 | sales_D13 | sales_D16 | sales_D18 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | SEP78 | 112 | 1.00000 | 1.01328 | 110.532 | 1.00000 | 1.00000 | 110.532 | 124.138 | 0.89040 | . | 0.90264 | 122.453 | 124.448 | 0.98398 | 0.91463 | 1.01328 |
| 2 | OCT78 | 118 | 1.00000 | 0.99727 | 118.323 | 1.00000 | 1.00000 | 118.323 | 124.905 | 0.94731 | . | 0.94328 | 125.438 | 125.115 | 1.00258 | 0.94070 | 0.99727 |
| 3 | NOV78 | 132 | 1.00000 | 0.98960 | 133.388 | 1.00000 | 1.00000 | 133.388 | 125.646 | 1.06161 | . | 1.06320 | 125.459 | 125.723 | 0.99790 | 1.05214 | 0.98960 |
| 4 | DEC78 | 129 | 1.00000 | 1.00957 | 127.777 | 1.00000 | 1.00000 | 127.777 | 126.231 | 1.01225 | . | 0.99534 | 128.375 | 126.205 | 1.01720 | 1.00487 | 1.00957 |
| 5 | JAN79 | 121 | 1.00000 | 0.99408 | 121.721 | 1.00000 | 1.00000 | 121.721 | 126.557 | 0.96179 | . | 0.97312 | 125.083 | 126.479 | 0.98896 | 0.96735 | 0.99408 |
| 6 | FEB79 | 135 | 0.99115 | 0.99115 | 136.205 | 1.00000 | 1.00000 | 136.205 | 126.678 | 1.07521 | . | 1.05931 | 128.579 | 126.587 | 1.01574 | 1.04994 | 0.99115 |
| 7 | MAR79 | 148 | 1.00000 | 1.00966 | 146.584 | 1.00000 | 1.00000 | 146.584 | 126.825 | 1.15580 | . | 1.17842 | 124.391 | 126.723 | 0.98160 | 1.18980 | 1.00966 |
| 8 | APR79 | 148 | 1.00000 | 0.99279 | 149.075 | 1.00000 | 1.00000 | 149.075 | 127.038 | 1.17347 | . | 1.18283 | 126.033 | 126.902 | 0.99315 | 1.17430 | 0.99279 |
| 9 | MAY79 | 136 | 1.00000 | 0.99406 | 136.813 | 1.00000 | 1.00000 | 136.813 | 127.433 | 1.07360 | . | 1.06125 | 128.916 | 127.257 | 1.01303 | 1.05495 | 0.99406 |
| 10 | JUN79 | 119 | 1.00000 | 1.01328 | 117.440 | 1.00000 | 1.00000 | 117.440 | 127.900 | 0.91822 | . | 0.91663 | 128.121 | 127.747 | 1.00293 | 0.92881 | 1.01328 |
| 11 | JUL79 | 104 | 1.00000 | 0.99727 | 104.285 | 1.00000 | 1.00000 | 104.285 | 128.499 | 0.81156 | . | 0.81329 | 128.226 | 128.421 | 0.99848 | 0.81107 | 0.99727 |
| 12 | AUG79 | 118 | 1.00000 | 0.99678 | 118.381 | 1.00000 | 1.00000 | 118.381 | 129.253 | 0.91589 | . | 0.91135 | 129.897 | 129.316 | 1.00449 | 0.90841 | 0.99678 |
| 13 | SEP79 | 115 | 1.00000 | 1.00229 | 114.737 | 0.98630 | 0.99964 | 114.778 | 130.160 | 0.88151 | 0.88182 | 0.90514 | 126.761 | 130.347 | 0.97249 | 0.90722 | 1.00229 |
| 14 | OCT79 | 126 | 1.00000 | 0.99408 | 126.751 | 0.88092 | 1.00320 | 126.346 | 131.238 | 0.96581 | 0.96273 | 0.93820 | 135.100 | 131.507 | 1.02732 | 0.93264 | 0.99408 |
| 15 | NOV79 | 141 | 1.00000 | 1.00366 | 140.486 | 1.00000 | 1.00000 | 140.486 | 132.699 | 1.05869 | . | 1.06183 | 132.306 | 132.937 | 0.99525 | 1.06571 | 1.00366 |
| 16 | DEC79 | 135 | 1.00000 | 0.99872 | 135.173 | 1.00000 | 1.00000 | 135.173 | 134.595 | 1.00429 | . | 0.99339 | 136.072 | 134.720 | 1.01004 | 0.99212 | 0.99872 |
| 17 | JAN80 | 125 | 1.00000 | 0.99406 | 125.747 | 0.00000 | 0.95084 | 132.248 | 136.820 | 0.91906 | 0.96658 | 0.97481 | 128.996 | 136.763 | 0.94321 | 0.96902 | 0.99406 |
| 18 | FEB80 | 149 | 1.02655 | 1.03400 | 144.100 | 1.00000 | 1.00000 | 144.100 | 139.215 | 1.03509 | . | 1.06153 | 135.748 | 138.996 | 0.97663 | 1.09762 | 1.03400 |
| 19 | MAR80 | 170 | 1.00000 | 0.99872 | 170.217 | 1.00000 | 1.00000 | 170.217 | 141.559 | 1.20245 | . | 1.17965 | 144.295 | 141.221 | 1.02177 | 1.17814 | 0.99872 |
| 20 | APR80 | 170 | 1.00000 | 0.99763 | 170.404 | 1.00000 | 1.00000 | 170.404 | 143.777 | 1.18520 | . | 1.18499 | 143.802 | 143.397 | 1.00283 | 1.18218 | 0.99763 |
| 21 | MAY80 | 158 | 1.00000 | 1.00966 | 156.489 | 1.00000 | 1.00000 | 156.489 | 145.925 | 1.07239 | . | 1.06005 | 147.624 | 145.591 | 1.01397 | 1.07028 | 1.00966 |
| 22 | JUN80 | 133 | 1.00000 | 0.99279 | 133.966 | 1.00000 | 1.00000 | 133.966 | 148.133 | 0.90436 | . | 0.91971 | 145.662 | 147.968 | 0.98442 | 0.91307 | 0.99279 |
| 23 | JUL80 | 114 | 1.00000 | 0.99406 | 114.681 | 0.00000 | 0.94057 | 121.927 | 150.682 | 0.76108 | 0.80917 | 0.81275 | 141.103 | 150.771 | 0.93588 | 0.80792 | 0.99406 |
Copyright © 2008 by SAS Institute Inc., Cary, NC, USA. All rights reserved.
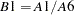 *
* 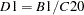 **
** 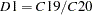
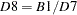 ***
*** 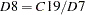
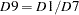 ;
; 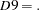 otherwise
otherwise 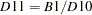 ****
**** 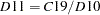
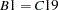 for this example
for this example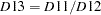
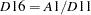
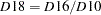
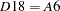 *****
*****