The seasonal component of this time series, 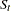, is defined as the intrayear variation that is repeated constantly (stable) or in an evolving fashion from year to year (moving seasonality). If the increase in the seasonal factors from year to year is too large, then the seasonal factors will introduce distortion into the model. It is important to determine if seasonality is identifiable without distorting the series.

For seasonality to be identifiable, the series should be identified as seasonal by using the "Test for the Presence of Seasonality Assuming Stability" and "Nonparametric Test for the Presence of Seasonality Assuming Stability." Also, since the presence of moving seasonality can cause distortion, it is important to evaluate the moving seasonality in conjunction with the stable seasonality to determine if the seasonality is identifiable.

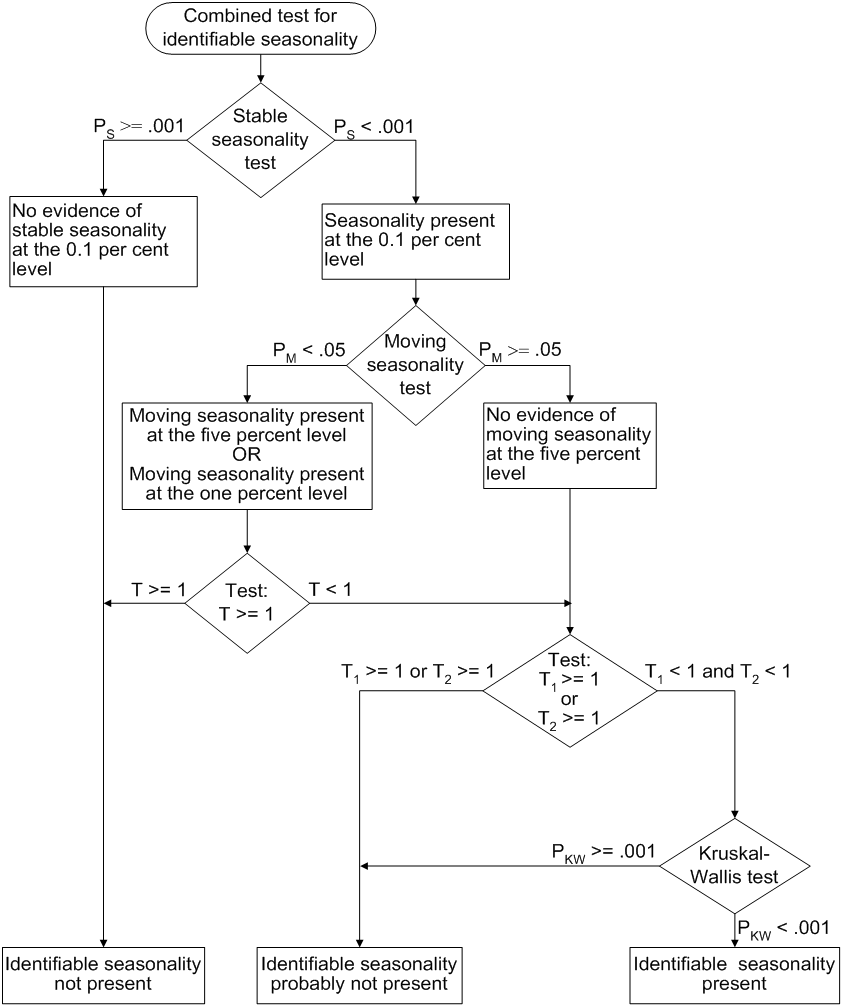
The test for identifiable seasonality is performed by combining the F tests for stable and moving seasonality, along with a Kruskal-Wallis test for stable seasonality. The description below is based on Lothian and Morry (1978b); other details can be found in Dagum (1988, 1983).

Let 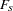and 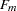denote the F value for the stable and moving seasonality tests, respectively. The combined test is performed as shown in Figure 32.3 and as follows:

1. If the null hypothesis in the stable seasonality test is not rejected at the 0.10% significance level (0.001), then since the series is not seasonal, PROC X12 displays "Identifiable Seasonality Not Present."

2. If the null hypothesis in step 1 is rejected, then compute the following quantities:

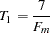
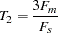
   Let denote the simple average of 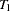and :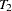

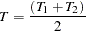
   If the moving seasonality null hypothesis is not rejected at the 5.0% significance level (0.05) and if 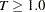, the null hypothesis of identifiable seasonality not present is accepted and PROC X12 displays "Identifiable Seasonality Not Present."

3. If the null hypothesis of identifiable seasonality not present has not been accepted, but 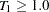, , 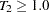or the Kruskal-Wallis chi-squared test fails at the 0.10% significance level (0.001), then PROC X12 displays "Identifiable Seasonality Probably Not Present."

4. If the 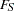and Kruskal-Wallis chi-squared tests pass, and if none of the combined measures described in steps 2 and 3 fail, then the null hypothesis of identifiable seasonality not present is rejected, and PROC X12 displays "Identifiable Seasonality Present."

The "Summary of Results for Combined Test for the Presence of Identifiable Seasonality" table displays the 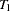, , 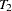and values and the significance levels for the stable seasonality test, the moving seasonality test, and the Kruskal-Wallis test. The last item in the table is the result of the combined test for identifiable seasonality.

Figure 32.3 Combined Seasonality Test Flowchart