| The VARMAX Procedure |
| Parameter Estimation and Testing on Restrictions |
In the previous example, the VARX(1,0) model is written as
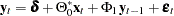 |
with
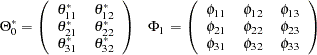 |
In Figure 30.20 of the preceding section, you can see several insignificant parameters. For example, the coefficients XL0_1_2, AR1_1_2, and AR1_3_2 are insignificant.
The following statements restrict the coefficients of  for the VARX(1,0) model.
for the VARX(1,0) model.
/*--- Models with Restrictions and Tests ---*/
proc varmax data=grunfeld;
model y1-y3 = x1 x2 / p=1 print=(estimates);
restrict XL(0,1,2)=0, AR(1,1,2)=0, AR(1,3,2)=0;
run;
The output in Figure 30.21 shows that three parameters 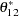 ,
, 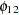 , and
, and 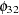 are replaced by the restricted values, zeros. In the schematic representation of parameter estimates, the three restricted parameters
are replaced by the restricted values, zeros. In the schematic representation of parameter estimates, the three restricted parameters 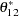 ,
, 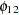 , and
, and 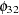 are replaced by
are replaced by  .
.
| XLag | |||
|---|---|---|---|
| Lag | Variable | x1 | x2 |
| 0 | y1 | 1.67592 | 0.00000 |
| y2 | -6.30880 | 2.65308 | |
| y3 | -0.03576 | -0.00919 | |
| AR | ||||
|---|---|---|---|---|
| Lag | Variable | y1 | y2 | y3 |
| 1 | y1 | 0.27671 | 0.00000 | 0.01747 |
| y2 | -2.16968 | 0.10945 | -0.93053 | |
| y3 | 0.96398 | 0.00000 | 0.93412 | |
| Schematic Representation | |||
|---|---|---|---|
| Variable/Lag | C | XL0 | AR1 |
| y1 | . | +* | .*. |
| y2 | + | .+ | ..- |
| y3 | - | .. | +*+ |
| + is > 2*std error, - is < -2*std error, . is between, * is N/A | |||
The output in Figure 30.22 shows the estimates of the Lagrangian parameters and their significance. Based on the  -values associated with the Lagrangian parameters, you cannot reject the null hypotheses
-values associated with the Lagrangian parameters, you cannot reject the null hypotheses 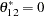 ,
, 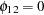 , and
, and 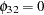 with the 0.05 significance level.
with the 0.05 significance level.
The TEST statement in the following example tests 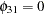 and
and  for the VARX(1,0) model:
for the VARX(1,0) model:
proc varmax data=grunfeld;
model y1-y3 = x1 x2 / p=1;
test AR(1,3,1)=0;
test XL(0,1,2)=0, AR(1,1,2)=0, AR(1,3,2)=0;
run;
The output in Figure 30.23 shows that the first column in the output is the index corresponding to each TEST statement. You can reject the hypothesis test 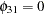 at the 0.05 significance level, but you cannot reject the joint hypothesis test
at the 0.05 significance level, but you cannot reject the joint hypothesis test  at the 0.05 significance level.
at the 0.05 significance level.
| Testing of the Parameters | |||
|---|---|---|---|
| Test | DF | Chi-Square | Pr > ChiSq |
| 1 | 1 | 150.31 | <.0001 |
| 2 | 3 | 0.34 | 0.9522 |
Copyright © 2008 by SAS Institute Inc., Cary, NC, USA. All rights reserved.