Previous Page | Next Page

The VARMAX Procedure
Vector Autoregressive Process

Let 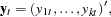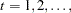denote a 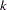-dimensional time series vector of random variables of interest. The th-order VAR process is written as

     

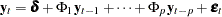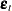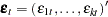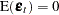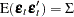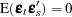where the is a vector white noise process with such that , , and for 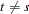; 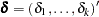is a constant vector and 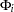is a 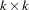matrix.

Analyzing and modeling the series jointly enables you to understand the dynamic relationships over time among the series and to improve the accuracy of forecasts for individual series by using the additional information available from the related series and their forecasts.

Example of Vector Autoregressive Model

Consider the first-order stationary bivariate vector autoregressive model

     

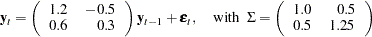The following IML procedure statements simulate a bivariate vector time series from this model to provide test data for the VARMAX procedure: 

   proc iml;
      sig = {1.0  0.5, 0.5 1.25};
      phi = {1.2 -0.5, 0.6 0.3};
      /* simulate the vector time series */
      call varmasim(y,phi) sigma = sig n = 100 seed = 34657;
      cn = {'y1' 'y2'};
      create simul1 from y[colname=cn];
      append from y;
   quit;

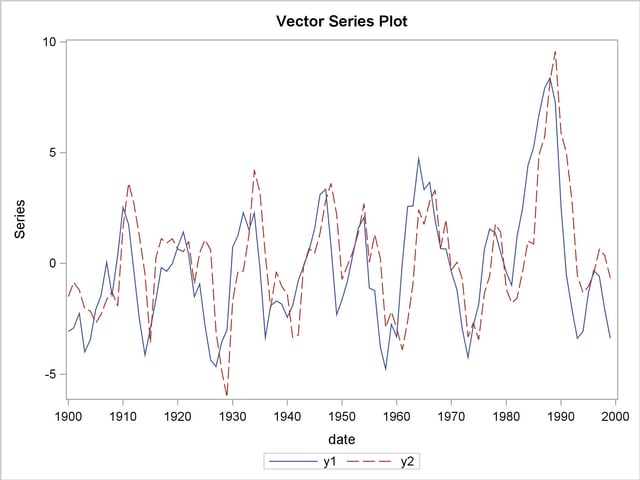
The following statements plot the simulated vector time series shown in Figure 30.1: 

   data simul1;
      set simul1;
      date = intnx( 'year', '01jan1900'd, _n_-1 );
      format date year4.;
   run;
   
   proc timeseries data=simul1 vectorplot=series;
      id date interval=year;
      var y1 y2;
   run;

Figure 30.1 Plot of Generated Data Process
Plot of Generated Data Process

The following statements fit a VAR(1) model to the simulated data. First, you specify the input data set in the PROC VARMAX statement. Then, you use the MODEL statement to designate the dependent variables, 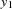and 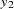. To estimate a VAR model with mean zero, you specify the order of the autoregressive model with the P= option and the NOINT option. The MODEL statement fits the model to the data and prints parameter estimates and their significance. The PRINT=ESTIMATES option prints the matrix form of parameter estimates, and the PRINT=DIAGNOSE option prints various diagnostic tests. The LAGMAX=3 option is used to print the output for the residual diagnostic checks.

To output the forecasts to a data set, you specify the OUTPUT statement with the OUT= option. If you want to forecast five steps ahead, you use the LEAD=5 option. The ID statement specifies the yearly interval between observations and provides the Time column in the forecast output.

The VARMAX procedure output is shown in Figure 30.2 through Figure 30.10. 

   /*--- Vector Autoregressive Model ---*/
   
   proc varmax data=simul1;
      id date interval=year;
      model y1 y2 / p=1 noint lagmax=3
                    print=(estimates diagnose);
      output out=for lead=5;
   run;

Figure 30.2 Descriptive Statistics
The VARMAX Procedure

Number of Observations 100
Number of Pairwise Missing 0

Simple Summary Statistics
Variable Type N Mean Standard
Deviation		 Min Max
y1 Dependent 100 -0.21653 2.78210 -4.75826 8.37032
y2 Dependent 100 0.16905 2.58184 -6.04718 9.58487

The VARMAX procedure first displays descriptive statistics. The Type column specifies that the variables are dependent variables. The column N stands for the number of nonmissing observations.

Figure 30.3 shows the type and the estimation method of the fitted model for the simulated data. It also shows the AR coefficient matrix in terms of lag 1, the parameter estimates, and their significance, which can indicate how well the model fits the data.

The second table schematically represents the parameter estimates and allows for easy verification of their significance in matrix form.

In the last table, the first column gives the left-hand-side variable of the equation; the second column is the parameter name AR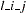, which indicates the (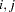)th element of the lag 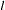autoregressive coefficient; the last column is the regressor that corresponds to the displayed parameter.

Figure 30.3 Model Type and Parameter Estimates
The VARMAX Procedure

Type of Model VAR(1)
Estimation Method Least Squares Estimation

AR
Lag Variable y1 y2
1 y1 1.15977 -0.51058
  y2 0.54634 0.38499

Schematic
Representation
Variable/Lag AR1
y1 +-
y2 ++
+ is > 2*std error,  - is < -2*std error,  . is between,  * is N/A

Model Parameter Estimates
Equation Parameter Estimate Standard
Error		 t Value Pr > |t| Variable
y1 AR1_1_1 1.15977 0.05508 21.06 0.0001 y1(t-1)
  AR1_1_2 -0.51058 0.05898 -8.66 0.0001 y2(t-1)
y2 AR1_2_1 0.54634 0.05779 9.45 0.0001 y1(t-1)
  AR1_2_2 0.38499 0.06188 6.22 0.0001 y2(t-1)

The fitted VAR(1) model with estimated standard errors in parentheses is given as

     

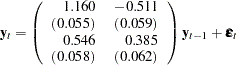Clearly, all parameter estimates in the coefficient matrix 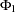are significant.

The model can also be written as two univariate regression equations.

     
     

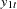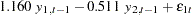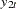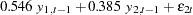The table in Figure 30.4 shows the innovation covariance matrix estimates and the various information criteria results. The smaller value of information criteria fits the data better when it is compared to other models. The variable names in the covariance matrix are printed for convenience; means the innovation for , and 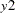means the innovation for .

Figure 30.4 Innovation Covariance Estimates and Information Criteria
Covariances of Innovations
Variable y1 y2
y1 1.28875 0.39751
y2 0.39751 1.41839

Information Criteria
AICC 0.554443
HQC 0.595201
AIC 0.552777
SBC 0.65763
FPEC 1.738092

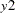Figure 30.5 shows the cross covariances of the residuals. The values of the lag zero are slightly different from Figure 30.4 due to the different degrees of freedom.

Figure 30.5 Multivariate Diagnostic Checks
Cross Covariances of Residuals
Lag Variable y1 y2
0 y1 1.24909 0.36398
  y2 0.36398 1.34203
1 y1 0.01635 0.03087
  y2 -0.07210 -0.09834
2 y1 0.06591 0.07835
  y2 0.01096 -0.05780
3 y1 -0.00203 0.08804
  y2 -0.02129 0.07277

Figure 30.6 and Figure 30.7 show tests for white noise residuals. The output shows that you cannot reject the null hypothesis that the residuals are uncorrelated.

Figure 30.6 Multivariate Diagnostic Checks Continued
Cross Correlations of Residuals
Lag Variable y1 y2
0 y1 1.00000 0.28113
  y2 0.28113 1.00000
1 y1 0.01309 0.02385
  y2 -0.05569 -0.07328
2 y1 0.05277 0.06052
  y2 0.00847 -0.04307
3 y1 -0.00163 0.06800
  y2 -0.01644 0.05422

Schematic Representation
of Cross Correlations
of Residuals
Variable/Lag 0 1 2 3
y1 ++ .. .. ..
y2 ++ .. .. ..
+ is > 2*std error,  - is < -2*std error,  . is between

Figure 30.7 Multivariate Diagnostic Checks Continued
Portmanteau Test for Cross Correlations
of Residuals
Up To Lag DF Chi-Square Pr > ChiSq
2 4 1.84 0.7659
3 8 2.57 0.9582

The VARMAX procedure provides diagnostic checks for the univariate form of the equations. The table in Figure 30.8 describes how well each univariate equation fits the data. From two univariate regression equations in Figure 30.3, the values of 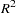in the second column are 0.84 and 0.80 for each equation. The standard deviations in the third column are the square roots of the diagonal elements of the covariance matrix from Figure 30.4. The 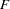statistics are in the fourth column for hypotheses to test 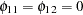and 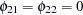, respectively, where 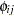is the 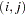th element of the matrix 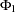. The last column shows the -values of the 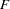statistics. The results show that each univariate model is significant.

Figure 30.8 Univariate Diagnostic Checks
Univariate Model ANOVA Diagnostics
Variable R-Square Standard
Deviation		 F Value Pr > F
y1 0.8369 1.13523 497.67 <.0001
y2 0.7978 1.19096 382.76 <.0001

The check for white noise residuals in terms of the univariate equation is shown in Figure 30.9. This output contains information that indicates whether the residuals are correlated and heteroscedastic. In the first table, the second column contains the Durbin-Watson test statistics to test the null hypothesis that the residuals are uncorrelated. The third and fourth columns show the Jarque-Bera normality test statistics and their -values to test the null hypothesis that the residuals have normality. The last two columns show 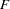statistics and their -values for ARCH(1) disturbances to test the null hypothesis that the residuals have equal covariances. The second table includes 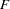statistics and their -values for AR(1), AR(1,2), AR(1,2,3) and AR(1,2,3,4) models of residuals to test the null hypothesis that the residuals are uncorrelated.

Figure 30.9 Univariate Diagnostic Checks Continued
Univariate Model White Noise Diagnostics
Variable Durbin
Watson		 Normality ARCH
Chi-Square Pr > ChiSq F Value Pr > F
y1 1.96656 3.32 0.1900 0.13 0.7199
y2 2.13609 5.46 0.0653 2.10 0.1503

Univariate Model AR Diagnostics
Variable AR1 AR2 AR3 AR4
F Value Pr > F F Value Pr > F F Value Pr > F F Value Pr > F
y1 0.02 0.8980 0.14 0.8662 0.09 0.9629 0.82 0.5164
y2 0.52 0.4709 0.41 0.6650 0.32 0.8136 0.32 0.8664

The table in Figure 30.10 gives forecasts, their prediction errors, and 95% confidence limits. See the section Forecasting for details.

Figure 30.10 Forecasts
Forecasts
Variable Obs Time Forecast Standard
Error		 95% Confidence Limits
y1 101 2000 -3.59212 1.13523 -5.81713 -1.36711
  102 2001 -3.09448 1.70915 -6.44435 0.25539
  103 2002 -2.17433 2.14472 -6.37792 2.02925
  104 2003 -1.11395 2.43166 -5.87992 3.65203
  105 2004 -0.14342 2.58740 -5.21463 4.92779
y2 101 2000 -2.09873 1.19096 -4.43298 0.23551
  102 2001 -2.77050 1.47666 -5.66469 0.12369
  103 2002 -2.75724 1.74212 -6.17173 0.65725
  104 2003 -2.24943 2.01925 -6.20709 1.70823
  105 2004 -1.47460 2.25169 -5.88782 2.93863

Previous Page | Next Page | Top of Page

Copyright © 2008 by SAS Institute Inc., Cary, NC, USA. All rights reserved.