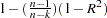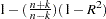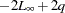This section explains the goodness-of-fit statistics reported to measure how well the specified model fits the data.

First the various statistics of fit that are computed using the prediction errors, 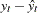, are considered. In these formulas, n is the number of nonmissing prediction errors and k is the number of fitted parameters in the model. Moreover, the sum of squared errors, , and the total sum of squares for the series corrected for the mean, , where is the series mean, and the sums are over all the nonmissing prediction errors.

Mean Squared Error
The mean squared prediction error,

Root Mean Squared Error
The root mean square error, RMSE =

Mean Absolute Percent Error
The mean absolute percent prediction error, MAPE = .
The summation ignores observations where .

R-square
The R-square statistic, .
If the model fits the series badly, the model error sum of squares, SSE, might be larger than SST and the R-square statistic will be negative.

Adjusted R-square
The adjusted R-square statistic,

Amemiya’s Adjusted R-square
Amemiya’s adjusted R-square,

Random Walk R-square
The random walk R-square statistic (Harvey’s R-square statistic that uses the random walk model for comparison), , where 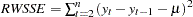, and

Maximum Percent Error
The largest percent prediction error, . In this computation the observations where are ignored.

The likelihood-based fit statistics are reported separately (see the section The UCMs as State Space Models). They include the full log likelihood (), the diffuse part of the log likelihood, the normalized residual sum of squares, and several information criteria: AIC, AICC, HQIC, BIC, and CAIC. Let denote the number of estimated parameters, be the number of nonmissing measurements in the estimation span, and 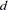be the number of diffuse elements in the initial state vector that are successfully initialized during the Kalman filtering process. Moreover, let 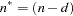. The reported information criteria, all in smaller-is-better form, are described in Table 29.4: